题目内容
6．命题“?x0∈R，使得x02+2x0+5＞0”的否定是?x∈R，都有x2+2x+5≤0．分析 根据特称命题的否定是全称命题即可得到结论．
解答 解：命题是特此命题，则命题的否定是：?x∈R，都有x2+2x+5≤0，
故答案为：?x∈R，都有x2+2x+5≤0
点评 本题主要考查含有量词的命题的否定，比较基础．
练习册系列答案
相关题目
17．
某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，其中正视图、侧视图中的两条虚线互相垂直，则该几何体的表面积是（ ）
某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，其中正视图、侧视图中的两条虚线互相垂直，则该几何体的表面积是（ ）| A． | 92 | B． | $16\sqrt{2}+80$ | C． | 80 | D． | $16\sqrt{2}+92$ |
14．若点P的坐标为（x0，y0），曲线C的方程为F（x，y）=0，则“F（x0，y0）=0”是“点P在曲线C上”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
1．若圆x2+y2-6x+6y+14=0关于直线l：ax+4y-6=0对称，则直线l的斜率是（ ）
| A． | 6 | B． | $\frac{2}{3}$ | C． | $-\frac{3}{2}$ | D． | -$\frac{2}{3}$ |
11．
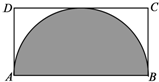如图所示，在矩形ABCD中，AB=2a，AD=a，图中阴影部分是以AB为直径的半圆，现在向矩形ABCD内随机撒4000粒豆子（豆子的大小忽略不计），根据你所学的概率统计知识，下列四个选项中最有可能落在阴影部分内的豆子数目是（ ）
如图所示，在矩形ABCD中，AB=2a，AD=a，图中阴影部分是以AB为直径的半圆，现在向矩形ABCD内随机撒4000粒豆子（豆子的大小忽略不计），根据你所学的概率统计知识，下列四个选项中最有可能落在阴影部分内的豆子数目是（ ）| A． | 1000 | B． | 2000 | C． | 3000 | D． | 4000 |
15．设f（x）的定义域为[0，1]，则f（2x-3）的定义域是（ ）
| A． | {x|x≥3} | B． | {x|-2≤x-1} | C． | {x|x≤-2} | D． | {x|log23≤x≤2} |