题目内容
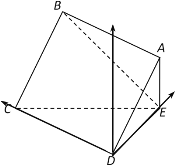
【题目】如图，在四棱锥E﹣ABCD中，底面ABCD是边长为2的正方形，且DE＝
，平面ABCD⊥平面ADE，∠ADE＝30°
（1）求证：AE⊥平面CDE；
（2）求AB与平面BCE所成角的正弦值.
【答案】（1）详见解析；（2）
.
【解析】
（1）根据线面垂直的判定定理，可直接得出结论成立；
（2）以
为原点，直线
，
分别为
轴，过点作与直线
平行的直线为
轴，建立空间直角坐标系，分别求出直线的方向向量与平面的法向量，根据向量夹角的余弦值，即可求出结果.
解：（1）证明：
平面
平面
，交线为
，且
平面，从而
，
又
，由 余弦定理得
，即
又
，
平面
.
（2）以为原点，直线
，分别为轴，过点作与直线平行的直线为轴，建立空间直角坐标系。
则
，
，
设
，
,
,
所以平面BCE的法向量
与平面
所成角的正弦弦值
练习册系列答案
相关题目
【题目】为了增强消防安全意识，某中学对全体学生做了一次消防知识讲座，从男生中随机抽取
人，从女生中随机抽取
人参加消防知识测试，统计数据得到如下列联表：
优秀 | 非优秀 | 总计 | |
男生 |
|
|
|
女生 |
|
|
|
总计 |
|
|
|
（1）试判断能否有
的把握认为消防知识的测试成绩优秀与否与性别有关；
附：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（2）为了宣传消防知识，从该校测试成绩获得优秀的同学中采用分层抽样的方法，随机选出
人组成宣传小组.现从这人中随机抽取
人到校外宣传，求到校外宣传的同学中男生人数
的分布列和数学期望.