题目内容
【题目】为了增强消防安全意识,某中学对全体学生做了一次消防知识讲座,从男生中随机抽取![]() 人,从女生中随机抽取
人,从女生中随机抽取![]() 人参加消防知识测试,统计数据得到如下列联表:
人参加消防知识测试,统计数据得到如下列联表:
优秀 | 非优秀 | 总计 | |
男生 |
|
|
|
女生 |
|
|
|
总计 |
|
|
|
(1)试判断能否有![]() 的把握认为消防知识的测试成绩优秀与否与性别有关;
的把握认为消防知识的测试成绩优秀与否与性别有关;
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
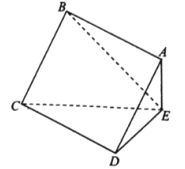
(2)为了宣传消防知识,从该校测试成绩获得优秀的同学中采用分层抽样的方法,随机选出![]() 人组成宣传小组.现从这
人组成宣传小组.现从这![]() 人中随机抽取
人中随机抽取![]() 人到校外宣传,求到校外宣传的同学中男生人数
人到校外宣传,求到校外宣传的同学中男生人数![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1) 没有![]() 的把握认为测试成绩优秀与否与性别有关(2)见解析
的把握认为测试成绩优秀与否与性别有关(2)见解析
【解析】
⑴将表中数据代入公式,对比对立性检验临界值表,即可得到结论
⑵根据古典概型的计算方法计算出![]() 可能的取值为
可能的取值为![]() 的概率,写出分布列,计算出期望即可
的概率,写出分布列,计算出期望即可
(1)因为![]() 的观测值
的观测值
![]()
![]() ,
,
所以没有![]() 的把握认为测试成绩优秀与否与性别有关.
的把握认为测试成绩优秀与否与性别有关.
(2)用分层抽样的方法抽取时抽取比例是![]() ,
,
则抽取女生![]() 人,抽取男生
人,抽取男生![]() 人.
人.
依题意,![]() 可能的取值为
可能的取值为![]() ,
,![]() ,
,![]() .
.
![]() ;
;![]() ;
;
![]() .
.
![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
![]() 的数学期望为:
的数学期望为:![]() .
.

【题目】某省为了了解和掌握2019年高考考生的实际答卷情况,随机地取出了100名考生的数学成绩,数据如下:(单位:分)
135 | 98 | 102 | 110 | 99 | 121 | 110 | 96 | 100 | 103 |
125 | 97 | 117 | 113 | 110 | 92 | 102 | 109 | 104 | 112 |
105 | 124 | 87 | 131 | 97 | 102 | 123 | 104 | 104 | 128 |
109 | 123 | 111 | 103 | 105 | 92 | 114 | 108 | 104 | 102 |
129 | 126 | 97 | 100 | 115 | 111 | 106 | 117 | 104 | 109 |
111 | 89 | 110 | 121 | 80 | 120 | 121 | 104 | 108 | 118 |
129 | 99 | 90 | 99 | 121 | 123 | 107 | 111 | 91 | 100 |
99 | 101 | 116 | 97 | 102 | 108 | 101 | 95 | 107 | 101 |
102 | 108 | 117 | 99 | 118 | 106 | 119 | 97 | 126 | 108 |
123 | 119 | 98 | 121 | 101 | 113 | 102 | 103 | 104 | 108 |
(1)列出频率分布表;
(2)画出频率分布直方图和折线图;
(3)估计该省考生数学成绩在![]() 分之间的比例.
分之间的比例.