题目内容
【题目】已知直线
，求：
(1)点P（4,5）关于l的对称点；
(2)直线x-y-2=0关于直线l对称的直线方程.
【答案】(1) （－2，7）(2) 7x＋y＋22＝0
【解析】
（1）设P（x，y）关于直线
：3x－y＋3＝0的对称点为
，则有
和PP'的中点在直线3x－y＋3＝0上，列方程组求解即可；
（2）将（1）中关于关于l的对称点的解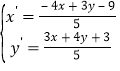
代入x－y－2＝0中的x，y即可得解.
(1)设P（x，y）关于直线：3x－y＋3＝0的对称点为则
∵，即
．①
又PP'的中点在直线3x－y＋3＝0上，
∴
．②
由①②得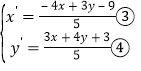
．
把x＝4，y＝5代入③④得
＝－2，
＝7，
∴P（4，5）关于直线的对称点
的坐标为（－2，7）．
（2）用③④分别代换x－y－2＝0中的x，y得关于的对称直线方程为
．
化简得7x＋y＋22＝0．
练习册系列答案
相关题目
【题目】某地区2007年至2013年农村居民家庭纯收入
（单位：千元）的数据如下表：
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）求y关于
的线性回归方程；
（2）判断y与之间是正相关还是负相关？
（3）预测该地区2015年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：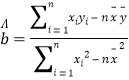
，
【题目】某校书法兴趣组有3名男同学A，B，C和3名女同学X，Y，Z，其年级情况如下表：
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加书法比赛
每人被选到的可能性相同
．
用表中字母列举出所有可能的结果；
设M为事件“选出的2人来自不同年级且性别相同”，求事件M发生的概率．
