题目内容
各项均为正数的数列{an}中,Sn是数列{an}的前n项和,且2Sn=an2+an,
(1)求数列{an}的通项公式;
(2)设c为实数,如果对任意的正整数n,不等式
-
>
恒成立,求证:c的最大值为1.
(1)求数列{an}的通项公式;
(2)设c为实数,如果对任意的正整数n,不等式
| an+2 |
| an |
| c | ||
|
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用an与sn的关系和题意得:(an+an-1)(an-an-1-1)=0,由an,>0的an-an-1-1=0,判断出数列{an}是等差数列,根据等差数列的通项公式求出an;
(2)由(1)和分子有理化化简
-
>
,得到c<
对对任意的正整数n恒成立,再求出
的范围,即可证明结论.
(2)由(1)和分子有理化化简
| an+2 |
| an |
| c | ||
|
| 2 | ||||
1+
|
| 2 | ||||
1+
|
解答:
解:(1)由题意得,2Sn=an2+an,且an,>0,①
当n=1时,2S1=a12+a1,解得a1=1或a1=0(舍去),
当n≥2时,2Sn-1=an-12+an-1,②
①-②得,2an=an2+an-an-12-an-1,
化简得,(an+an-1)(an-an-1-1)=0,
又an+an-1,>0,所以an-an-1-1=0,即an-an-1=1,
所以数列{an}是以1为首项、公差的等差数列,
则an=1+(n-1)=n;
证明:(2)由(1)得,
-
>
为:
-
>
,
即c<
(
-
)=
=
=
=
,
因为
<1,所以
>1,
因为不等式
-
>
对任意的正整数n恒成立,
即c<
对任意的正整数n恒成立,
所以c≤1,则c的最大值为1.
当n=1时,2S1=a12+a1,解得a1=1或a1=0(舍去),
当n≥2时,2Sn-1=an-12+an-1,②
①-②得,2an=an2+an-an-12-an-1,
化简得,(an+an-1)(an-an-1-1)=0,
又an+an-1,>0,所以an-an-1-1=0,即an-an-1=1,
所以数列{an}是以1为首项、公差的等差数列,
则an=1+(n-1)=n;
证明:(2)由(1)得,
| an+2 |
| an |
| c | ||
|
| n+2 |
| n |
| c | ||
|
即c<
| n+2 |
| n+2 |
| n |
| ||||||||||
|
=
2
| ||||
|
| 2 | ||||
1+
|
| 2 | ||||
1+
|
因为
1-
|
| 2 | ||||
1+
|
因为不等式
| an+2 |
| an |
| c | ||
|
即c<
| 2 | ||||
1+
|
所以c≤1,则c的最大值为1.
点评:本题考查数列an与sn的关系,等差数列的通项公式,不等式恒成立求参数范围转化为求范围问题,考查探索、分析及论证的能力.

练习册系列答案
相关题目
给出以下四个命题:
①若x,y∈N*,x+y是奇数,则x,y中一个是奇数一个是偶数;
②若-2≤x<3,则(x+2)(x-3)≤0;
③若x=y=0,则x2+y2=0;
④若x2-3x+2=0,则x=1或x=2.
那么( )
①若x,y∈N*,x+y是奇数,则x,y中一个是奇数一个是偶数;
②若-2≤x<3,则(x+2)(x-3)≤0;
③若x=y=0,则x2+y2=0;
④若x2-3x+2=0,则x=1或x=2.
那么( )
| A、①为假命题 |
| B、②的否命题为真 |
| C、③的逆否命题为假 |
| D、④的逆命题为真 |
下列说法错误的是( )
| A、已知命题p为“?x∈[0,+∞),(log32)x≤1”,则¬p是真命题 |
| B、若p∨q为假命题,则p、q均为假命题 |
| C、x>2是x>1充分不必要条件 |
| D、“全等三角形的面积相等”的否命题是假命题 |
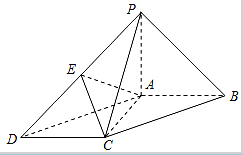 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.