Question

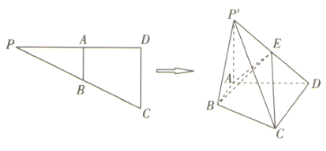
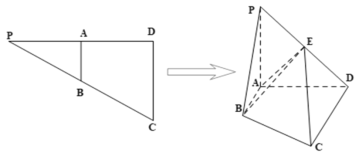
【题目】如图在三棱锥中，和均为等腰三角形，且，．

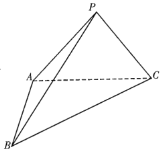
（1）判断是否成立？并给出证明；

（2）求直线与平面所成角的正弦值．

Answer 1

【答案】（1）不成立，证明见解析；（2）.

【解析】

（1）假设，得平面，由线面垂直的性质可得，与矛盾，从而可得不成立；

（2）取的中点，的中点，证明平面，进而可得平面平面，再取的中点，证明平面，根据线面角的定义知为直线与平面所成的角，在直角三角形中求解．

（1）不成立，证明如下：

假设，因为，且，

所以平面，

所以，这与已知矛盾，

所以不成立．

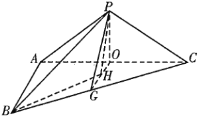
（2）如图，取的中点，的中点，连接，，，

由已知计算得，

由已知得，，且，

所以平面，所以平面平面．

取的中点，连接，，

则，平面，从而是直线与平面所成的角，

因为，，所以，即直线与平面所成角的正弦值为．