题目内容
已知椭圆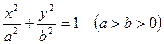 的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
(1)求椭圆的标准方程;
(2)设M为右顶点,则直线AM、BM与准线l分别交于P、Q两点,(P、Q两点不重合),求证: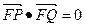
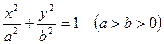 的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。(1)求椭圆的标准方程;
(2)设M为右顶点,则直线AM、BM与准线l分别交于P、Q两点,(P、Q两点不重合),求证:
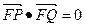
(1)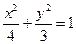
(2)见解析
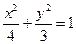
(2)见解析
(1)由题意有
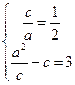 解得
解得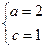
∴椭圆的标准方程为
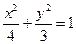 ……………………………………5分
……………………………………5分(2)①若直线AB与
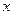 轴垂直,则直线AB的方程是
轴垂直,则直线AB的方程是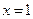
∵该椭圆的准线方程为
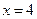 ,
,∴
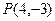 ,
, ,∴
,∴ ,
,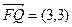
∴
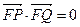 ∴当直线AB与
∴当直线AB与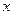 轴垂直时,命题成立。
轴垂直时,命题成立。②若直线AB与
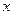 轴不垂直,则设直线AB的斜率为
轴不垂直,则设直线AB的斜率为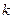 ,
,∴直线AB的方程为
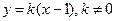
又设
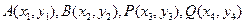
联立
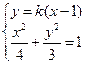 消y得
消y得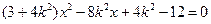
∴
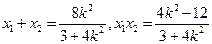 ∴
∴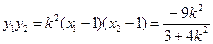
又∵A、M、P三点共线,∴
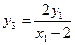 同理
同理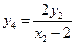
∴
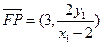 ,
,
∴
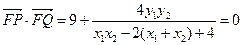
综上所述:

练习册系列答案
相关题目
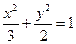 的左、右焦点分别为
的左、右焦点分别为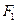 ,
,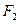 .过
.过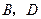 两点,过
两点,过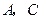 两点,且
两点,且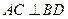 ,垂足为
,垂足为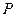 .
.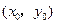 ,证明:
,证明: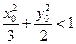 ;
;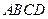 的面积的最小值.
的面积的最小值.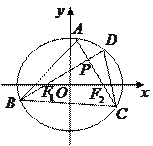
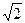 ,BC=1.以AB的中点
,BC=1.以AB的中点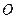 为原点建立如图8所示的平面直角坐标系
为原点建立如图8所示的平面直角坐标系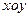 .
.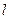 交(Ⅰ)中椭圆于M,N两点,是否存在直线
交(Ⅰ)中椭圆于M,N两点,是否存在直线
 过点(1,
过点(1, 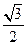 ),F1、F2分别为其左、右焦点,且离心率e=
),F1、F2分别为其左、右焦点,且离心率e=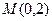 的直线
的直线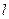 与椭圆C交于不同的两点
与椭圆C交于不同的两点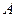 、
、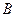 ,且∠
,且∠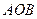 为锐角(其中
为锐角(其中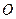 为坐标原点),求直线
为坐标原点),求直线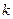 的取值范围.
的取值范围. 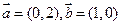 ,过定点
,过定点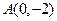 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点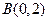 ,以向量
,以向量 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
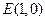 的直线
的直线 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求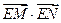 的取值范围
的取值范围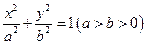 的中心在坐标原点
的中心在坐标原点 ,一条准线的方程为
,一条准线的方程为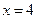 ,过椭圆的左焦点
,过椭圆的左焦点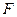 ,且方向向量为
,且方向向量为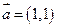 的直线
的直线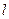 交椭圆于
交椭圆于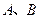 两点,
两点,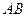 的中点为
的中点为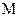
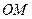 的斜率(用
的斜率(用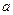 、
、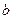 表示);
表示);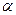 ,当
,当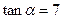 时,求椭圆的方程.
时,求椭圆的方程. 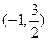 ;
;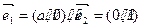 ,经过定点
,经过定点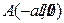 且方向向量为
且方向向量为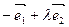 的直线与经过定点
的直线与经过定点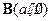 且方向向量为
且方向向量为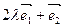 的直线交于点M,其中
的直线交于点M,其中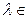 R,常数a>0.
R,常数a>0.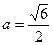 ,过点
,过点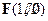 的直线与点M的轨迹交于C、D两点,求
的直线与点M的轨迹交于C、D两点,求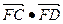 的取值范围.
的取值范围.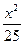 +
+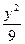 ="1"
="1"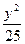 +
+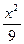 =1(y≠0)
=1(y≠0)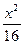 +
+