题目内容
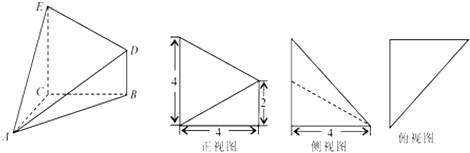
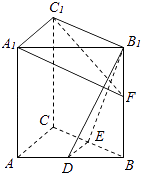
【题目】如图，在矩形ABCD中，AB=8，BC=4，E为DC边的中点，沿AE将△ADE折起，在折起过程中，有几个正确（ ）
①ED⊥平面ACD ②CD⊥平面BED ③BD⊥平面ACD ④AD⊥平面BED．
A.1个
B.2个
C.3个
D.4个
【答案】A
【解析】解：∵在矩形ABCD中，AB=8，BC=4，E为DC边的中点，
∴在折起过程中，D点在平面BCE上的投影如右图．
∵DE与AC所成角不能为直角，
∴DE不会垂直于平面ACD，故①错误；
只有D点投影位于O2位置时，即平面AED与平面AEB重合时，
才有BE⊥CD，此时CD不垂直于平面AEBC，
故CD与平面BED不垂直，故②错误；
BD与AC所成角不能成直线，
∴BD不能垂直于平面ACD，故③错误；
∵AD⊥ED，并且在折起过程中，有AD⊥BC，
∴存在一个位置使AD⊥BE，
∴在折起过程中AD⊥平面BED，故④正确．
故选：A．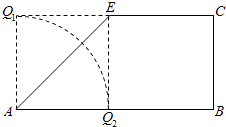
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．
天天向上口算本系列答案
【题目】某校从参加高三期中考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），数学成绩分组及样本频率分布表如下：
分组 | 频数 | 频率 |
[40，50） | 2 | 0.04 |
[50，60） | 3 | 0.06 |
[60，70） | 14 | 0.28 |
[70，80） | 15 | ② |
[80，90） | ① | 0.24 |
[90，100] | 4 | 0.08 |
合计 | ③ | ④ |
（1）请把给出的样本频率分布表中的空格都填上；
（2）为了帮助成绩差的学生提高数学成绩，学校决定成立“二帮一”小组，即从成绩[90，100]中选两位同学，共同帮助[40，50）中的某一位同学，已知甲同学的成绩为42分，乙同学的成绩为95分，求甲、乙两同学恰好被安排在同一小组的概率．
【题目】某特色餐馆开通了美团外卖服务，在一周内的某特色菜外卖份数
（份）与收入
（元）之间有如下的对应数据：
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
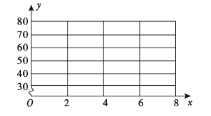
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计外卖份数为12份时，收入为多少元．
注：①参考公式：线性回归方程系数公式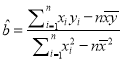
， 
；
②参考数据： 
， 
， 
．
