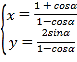题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)讨论![]() 的单调性;
的单调性;
(2)若对![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)①当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;②当
上单调递增;②当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
(2)![]() .
.
【解析】
(1)求出函数的定义域和导函数, ![]() ,对
,对![]() 讨论,得导函数的正负,得原函数的单调性;(2)法一: 由
讨论,得导函数的正负,得原函数的单调性;(2)法一: 由![]() 得
得![]() ,
,
分别运用导函数得出函数![]() (
(![]() ),
),![]() 的单调性,和其函数的最值,可得
的单调性,和其函数的最值,可得![]() ,可得的范围;
,可得的范围;
法二:由![]() 得
得![]() ,化为
,化为![]() 令
令![]() (
(![]() ),研究函数的单调性,可得
),研究函数的单调性,可得![]() 的取值范围.
的取值范围.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①当![]() 时,由
时,由![]() 得
得![]() ,
,![]() 得
得![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增;
上单调递增;
(2)法一: 由![]() 得
得![]() ,
,
令![]() (
(![]() ),则
),则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,
令![]() ,
,
则![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() ,
,
![]() (*)
(*)
当![]() 时,
时,![]() ,
,![]() (*)式恒成立,即
(*)式恒成立,即![]() 恒成立,满足题意
恒成立,满足题意
法二:由![]() 得
得![]() ,
,![]() ,
,![]()
令![]() (
(![]() ),则
),则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,
当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() 在
在![]() 上单调递增,
上单调递增,![]() 恒成立,满足题意
恒成立,满足题意
当![]() 时,令
时,令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,使得
,使得![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,![]() ,不满足题意,
,不满足题意,
综上所述,![]() 的取值范围是
的取值范围是![]()

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
【题目】某校高一年级有甲,乙,丙三位学生,他们前三次月考的物理成绩如表:
第一次月考物理成绩 | 第二次月考物理成绩 | 第三次月考物理成绩 | |
学生甲 | 80 | 85 | 90 |
学生乙 | 81 | 83 | 85 |
学生丙 | 90 | 86 | 82 |
则下列结论正确的是( )
A. 甲,乙,丙第三次月考物理成绩的平均数为86
B. 在这三次月考物理成绩中,甲的成绩平均分最高
C. 在这三次月考物理成绩中,乙的成绩最稳定
D. 在这三次月考物理成绩中,丙的成绩方差最大