题目内容
【题目】老王有一块矩形旧铁皮
，其中
，
，他想充分利用这块铁皮制作一个容器，他有两个设想：设想1是沿矩形的对角线
把
折起，使
移到
点，且在平面
上的射影
恰好在
上，再利用新购铁皮缝制其余两个面得到一个三棱锥
；设想2是利用旧铁皮做侧面，新购铁皮做底面，缝制一个高为
，侧面展开图恰为矩形的圆柱体；
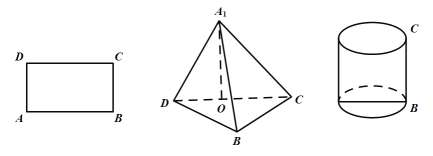
（1）求设想1得到的三棱锥
中二面角
的大小；
（2）不考虑其他因素，老王的设想1和设想2分别得到的几何体哪个容积更大？说明理由.
【答案】(1)
；(2) 圆柱体容积更大,证明见解析
【解析】
(1)过
做
,连接
.证明
为二面角
再计算其余弦值即可.
(2)分别计算三棱锥与圆柱体的体积,再比较大小即可.
(1)过做,连接.由题意可知
,根据三垂线定理知
.
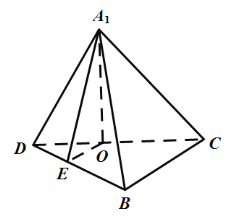
故为二面角.利用等面积法
.
解得
.进一步可求得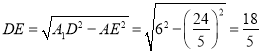
,
根据三角形相似有
,解得
.
故在
中, 
.
所以
.
即二面角的大小为
(2)棱锥体积
圆柱体积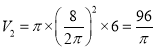
.
因为
.故圆柱体容积更大.
练习册系列答案
相关题目
