题目内容
【题目】记无穷数列![]() 的前n项
的前n项![]() ,
,![]() ,…,
,…,![]() 的最大项为
的最大项为![]() ,第n项之后的各项
,第n项之后的各项![]() ,
,![]() ,…的最小项为
,…的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,写出
,写出![]() ,
,![]() ,并求数列
,并求数列![]() 通项公式;
通项公式;
(2)若数列![]() 的通项公式为
的通项公式为![]() ,判断
,判断![]() 是否为等差数列,若是,求出公差;若不是,请说明理由;
是否为等差数列,若是,求出公差;若不是,请说明理由;
(3)若数列![]() 为公差大于零的等差数列,求证:
为公差大于零的等差数列,求证:![]() 是等差数列.
是等差数列.
【答案】(1)![]() ,
,![]() ,
,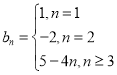 ;(2)是等差数列,公差
;(2)是等差数列,公差![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)利用![]() 和
和![]() 表示出数列
表示出数列![]() 即可;
即可;
(2)根据![]() ,求出数列
,求出数列![]() 的单调性,进而求出
的单调性,进而求出![]() 的通项公式,确定数列类型;
的通项公式,确定数列类型;
(3)根据数列![]() 为公差大于零的等差数列,可以设数列
为公差大于零的等差数列,可以设数列![]() 的通项公式,然后求出数列
的通项公式,然后求出数列![]() 的单调性,进而表示出
的单调性,进而表示出![]() 的通项公式.
的通项公式.
(1)由题知数列![]() 的通项公式为
的通项公式为![]() ,在
,在![]() 时是单调递增数列,
时是单调递增数列,
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() ,
,
当![]() 时,数列
时,数列![]() 为单调递增数列,
为单调递增数列,
所以![]() ,
,![]() ,
,
故![]() ,
,
整理得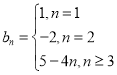 .
.
(2)由题知数列![]() 的通项公式为
的通项公式为![]() ,
,
所以数列![]() 是单调递减的数列,且
是单调递减的数列,且![]() ,
,
由题知![]() ,
,![]() ,
,
因为![]() ,
,
故数列![]() 是单调递增数列,
是单调递增数列,
所以当![]() 时,
时,![]() ,
,![]() ,
,
故![]() ,
,
所以数列![]() 的通项公式是
的通项公式是![]() ,
,
即数列![]() 是等差数列,公差
是等差数列,公差![]() .
.
(3)由题知数列![]() 为公差大于零的等差数列,
为公差大于零的等差数列,
故设![]() 且公差
且公差![]() ,
,
当![]() 时,有
时,有![]() ,
,
整理得![]() ,
,
若![]() ,则有
,则有![]() ,
,
故![]() ,
,
因为![]() ,所以当
,所以当![]() 时
时![]() ,
,
当![]() 时
时![]() ,
,
类似的可以证明![]() ,
,
因为![]() ,
,
故有![]() ,
,
故数列![]() 是单调递增数列,
是单调递增数列,
所以当![]() 时,
时,![]() ,
,![]() ,
,
故![]() ,
,
所以数列![]() 的通项公式是
的通项公式是![]() ,
,
即数列![]() 是等差数列,公差为
是等差数列,公差为![]() .
.

【题目】某医院体检中心为回馈大众,推出优惠活动:对首次参加体检的人员,按200元次收费,并注册成为会员,对会员的后续体检给予相应优惠,标准如下:
体检次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次及以上 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.8 |
该体检中心从所有会员中随机选取了100位对他们在本中心参加体检的次数进行统计,得到数据如下表:
体检次数 | 一次 | 两次 | 三次 | 四次 | 五次及以上 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设该体检中心为顾客体检一次的成本费用为150元,根据所给数据,解答下列问题:
(1)该体检中心要从这100人里至少体检3次的会员中,按体检次数用分层抽样的方法抽出8人,再从这8人中抽出2人发放纪念品,求抽出的2人中恰有1人体检3次的概率;
(2)若以这100位会员体检次数的频率分布估计该体检中心所有会员体检次数的概率分布,已知该中心本周共接待了1000名顾客参加体检,试估计该体检中心本周所获利润.