题目内容
平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设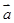 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an),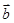 =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量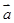 与
与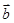 夹角θ的余弦为cosθ=
夹角θ的余弦为cosθ=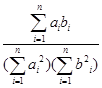 .已知n维向量
.已知n维向量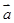 ,
,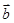 ,当
,当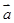 =(1,1,1,1,…,1),
=(1,1,1,1,…,1),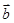 =(-1,-1,1,1,1,…,1)时,cosθ等于______________
=(-1,-1,1,1,1,…,1)时,cosθ等于______________
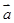 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an),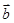 =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量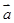 与
与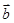 夹角θ的余弦为cosθ=
夹角θ的余弦为cosθ=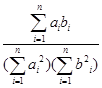 .已知n维向量
.已知n维向量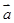 ,
,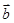 ,当
,当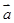 =(1,1,1,1,…,1),
=(1,1,1,1,…,1),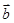 =(-1,-1,1,1,1,…,1)时,cosθ等于______________
=(-1,-1,1,1,1,…,1)时,cosθ等于______________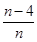
解:由题意对运算的推广得,cosθ即为向量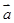 与
与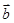 夹角θ的余弦,利用数量积公式解得为
夹角θ的余弦,利用数量积公式解得为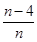
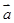 与
与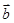 夹角θ的余弦,利用数量积公式解得为
夹角θ的余弦,利用数量积公式解得为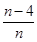

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
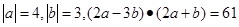 ,求
,求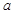 与
与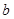 的夹角
的夹角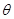 .
.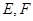 是等腰直角三角形
是等腰直角三角形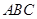 的斜边
的斜边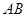 上的三等分点,则
上的三等分点,则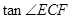 = ( )
= ( )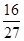
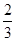
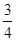
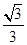
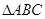 的内角
的内角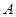 、
、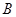 、
、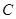 的对边分别为
的对边分别为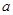 、
、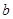 、
、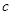 ,
,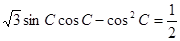 ,且
,且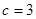
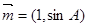 与
与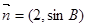 共线,求
共线,求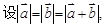 则
则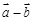 与
与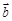 的夹角为 ( )
的夹角为 ( )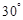
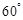
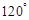
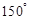
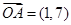 ,
,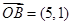 ,
,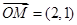 ,点
,点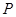 是直线
是直线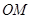 上的一个动点,且
上的一个动点,且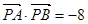 ,求
,求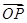 的坐标及
的坐标及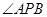 的余弦值.
的余弦值. 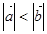 ,
,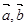 的夹角为
的夹角为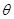 ,若函数
,若函数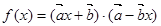 在
在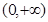 上单调,则
上单调,则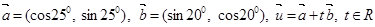 ,则|
,则|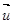 |的最小值是
|的最小值是
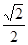
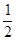
 且满足
且满足
 的坐标及向量
的坐标及向量 的夹角;
的夹角; 与
与 平行,求
平行,求 的值.
的值.