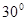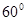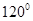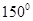题目内容
(本小题满分12分已知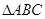 的内角
的内角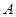 、
、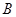 、
、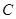 的对边分别为
的对边分别为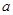 、
、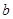 、
、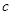 ,
,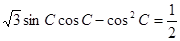 ,且
,且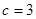
(1)求角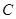 ;
;
(2)若向量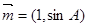 与
与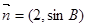 共线,求
共线,求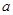 、
、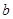 的值.
的值.
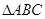 的内角
的内角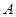 、
、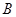 、
、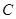 的对边分别为
的对边分别为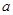 、
、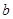 、
、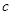 ,
,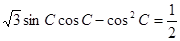 ,且
,且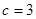
(1)求角
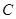 ;
;(2)若向量
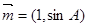 与
与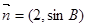 共线,求
共线,求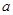 、
、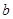 的值.
的值.(1)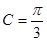 ;(2)
;(2)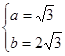 。
。
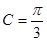 ;(2)
;(2)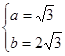 。
。本事主要是结合了向量共线来考查了解三角形的的运用。
(1)利用三角恒等变换化为关于角C的方程,求解得到角C。
(2)根据向量共线,得坐标关系,然后利用余弦定理和正弦定理得到边的长度。
解:(1)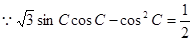
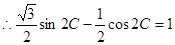 ,即
,即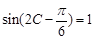 ,
,
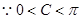 ,
,
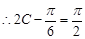 ,解得
,解得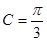
 ……5分
……5分
(2) 共线,
共线,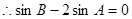 。
。
由正弦定理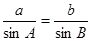 ,得
,得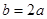 ,①……8分
,①……8分
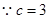 ,由余弦定理,得
,由余弦定理,得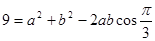 ,②
,②
联立方程①②,得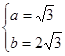 ……12分
……12分
(1)利用三角恒等变换化为关于角C的方程,求解得到角C。
(2)根据向量共线,得坐标关系,然后利用余弦定理和正弦定理得到边的长度。
解:(1)
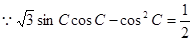
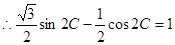 ,即
,即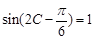 ,
,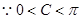 ,
,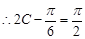 ,解得
,解得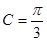
 ……5分
……5分(2)
 共线,
共线,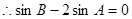 。
。由正弦定理
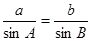 ,得
,得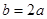 ,①……8分
,①……8分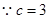 ,由余弦定理,得
,由余弦定理,得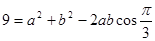 ,②
,②联立方程①②,得
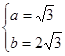 ……12分
……12分
练习册系列答案
相关题目
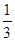 AB,则
AB,则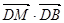 等于__________________.
等于__________________. 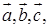 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为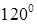 。
。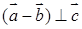 ;
;
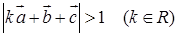 ,求
,求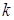 的取值范围。
的取值范围。 中,
中,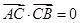
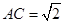 ,则
,则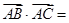 __________;
__________; 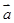 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an),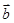 =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量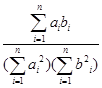 .已知n维向量
.已知n维向量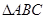 的面积为
的面积为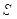 ,且
,且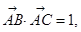 若
若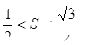 ,则
,则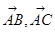 夹角的取值范围是( )
夹角的取值范围是( )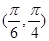
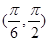
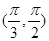
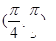
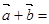 (1,2),
(1,2), ,且
,且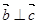 ,则
,则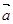 在
在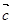 方向上的投影是( )
方向上的投影是( )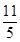
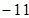

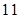
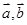 满足
满足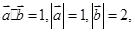 则向量
则向量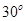
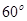
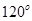
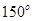
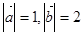 ,
,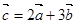 ,
,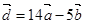 ,若
,若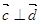 ,则
,则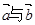 的夹角为( )
的夹角为( )