题目内容
设平面内的向量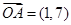 ,
,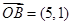 ,
,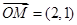 ,点
,点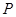 是直线
是直线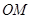 上的一个动点,且
上的一个动点,且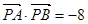 ,求
,求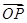 的坐标及
的坐标及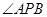 的余弦值.
的余弦值.
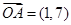 ,
,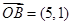 ,
,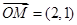 ,点
,点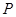 是直线
是直线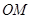 上的一个动点,且
上的一个动点,且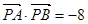 ,求
,求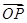 的坐标及
的坐标及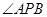 的余弦值.
的余弦值. 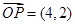 ,
,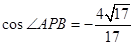
本题考查了向量共线的条件,向量的坐标运算,数量积的坐标表示,向量的模的求法及利用数量积计算夹角的余弦,本题综合性强,运算量大,谨慎计算是正确解题的关键
(1)设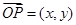 .
.
∵点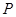 在直线
在直线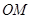 上,
上,
∴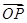 与
与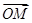 共线,而
共线,而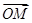
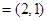 ,
,
∴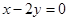 ,即
,即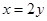 ,有
,有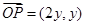
∴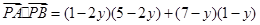 又
又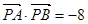 ,那么得到坐标,进而求解夹角的余弦值。
,那么得到坐标,进而求解夹角的余弦值。
解:设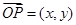 .
.
∵点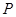 在直线
在直线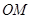 上,
上,
∴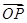 与
与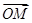 共线,而
共线,而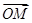
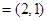 ,
,
∴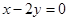 ,即
,即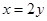 ,有
,有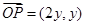 . ……………… 4分
. ……………… 4分
∵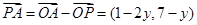 ,
,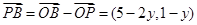 ,
,
∴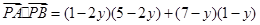 ,
,
即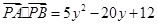 . 又
. 又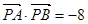 , ∴
, ∴ ,
,
所以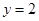 ,
,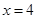 ,此时
,此时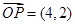 . ……………………8分
. ……………………8分
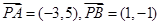 .
.
于是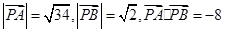 .
.
∴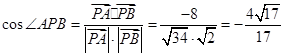 ………………12分
………………12分
(1)设
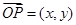 .
.∵点
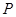 在直线
在直线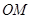 上,
上,∴
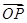 与
与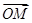 共线,而
共线,而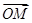
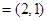 ,
,∴
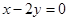 ,即
,即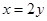 ,有
,有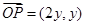
∴
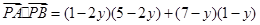 又
又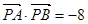 ,那么得到坐标,进而求解夹角的余弦值。
,那么得到坐标,进而求解夹角的余弦值。解:设
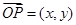 .
.∵点
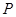 在直线
在直线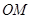 上,
上,∴
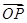 与
与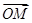 共线,而
共线,而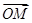
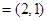 ,
,∴
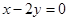 ,即
,即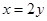 ,有
,有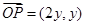 . ……………… 4分
. ……………… 4分 ∵
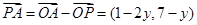 ,
,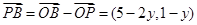 ,
, ∴
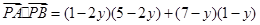 ,
,即
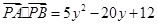 . 又
. 又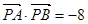 , ∴
, ∴ ,
,所以
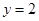 ,
,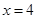 ,此时
,此时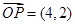 . ……………………8分
. ……………………8分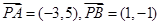 .
.于是
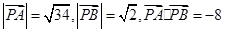 .
. ∴
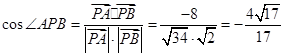 ………………12分
………………12分
练习册系列答案
相关题目
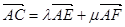 ,其中
,其中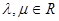 ,则
,则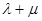 的值是
的值是


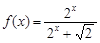 的图象上两点P1(x1,y1)、P2(x2,y2),若
的图象上两点P1(x1,y1)、P2(x2,y2),若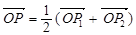 ,且点P的横坐标为
,且点P的横坐标为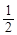 .
.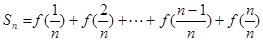
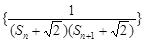 的前n项和,若
的前n项和,若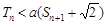 对一切n∈N*都成立,试求a的取值范围。
对一切n∈N*都成立,试求a的取值范围。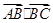 的值为( )
的值为( )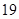
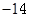
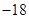
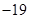
 中,
中,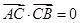
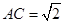 ,则
,则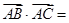 __________;
__________; 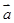 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an),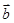 =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量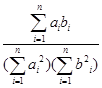 .已知n维向量
.已知n维向量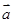 与
与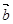 的夹角为120°,且|
的夹角为120°,且|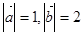 ,
,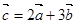 ,
,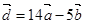 ,若
,若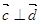 ,则
,则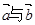 的夹角为( )
的夹角为( )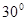
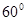
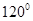
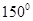
 与
与 的夹角为120°,且
的夹角为120°,且 ,则
,则 ______________
______________