题目内容
【题目】已知函数![]() 是
是![]() 上的偶函数.
上的偶函数.
(1)求![]() 值;
值;
(2)解![]() 的不等式的解集;
的不等式的解集;
(3)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)a=1;(2)(﹣2,2);(3)![]() .
.
【解析】
(1)根据函数的奇偶性求出a的值即可;
(2)设2x=t,则不等式即为![]() ,再解关于x的不等式即可;
,再解关于x的不等式即可;
(3)问题转化为m![]() 在(0,+∞)恒成立,设t=2x,(t>1),则m
在(0,+∞)恒成立,设t=2x,(t>1),则m![]() 在t>1恒成立,从而求出m的范围即可.
在t>1恒成立,从而求出m的范围即可.
(1)∵f(x)为偶函数,
∴f(﹣x)=f(x)恒成立,
∴f(﹣x)﹣f(x)=0恒成立,
∴![]() ,恒成立,
,恒成立,
即![]() 恒成立,
恒成立,
![]() ,
,
∵a>0,∴a=1,∴a=1;
(2)由(1)知![]() ,
,
设2x=t,则不等式即为![]() ,
,
∴![]() ,
,
所以原不等式解集为(﹣2,2);
(3)f(x)=2x+2﹣x﹣1,
mf(x)≥2﹣x﹣m,
即m![]() 在(0,+∞)恒成立,
在(0,+∞)恒成立,
设t=2x,(t>1),则m![]() 在t>1恒成立,
在t>1恒成立,
又y![]() 在t>1单调递减,得
在t>1单调递减,得![]()
故![]() .
.

练习册系列答案
相关题目
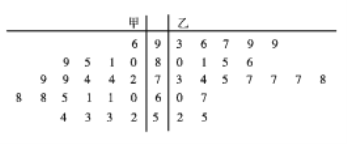
【题目】为推行“新课堂”教学法,某老师分别用传统教学和“新课堂”两种不同的教学方式在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,若成绩大于70分为“成绩优良”.
(1)由统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,求抽取的2人中恰有一人来自乙班的概率.
|
|
|
|
|
|
|
|
|
|
附:![]() ,(
,(![]() )
)



