题目内容
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)设![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() ,试确定
,试确定![]() 的值,使得二面角
的值,使得二面角![]() 的大小为
的大小为![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据线面垂直的判定定理,即可证明结论成立;
(2)先由(1)得![]() 两两垂直,以
两两垂直,以![]() 点为坐标原点,以
点为坐标原点,以![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正方向,建立空间直角坐标系,分别求出平面
轴正方向,建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的一个法向量,根据向量夹角余弦值与二面角的大小,即可求出结果.
的一个法向量,根据向量夹角余弦值与二面角的大小,即可求出结果.
(1)因为侧面![]() 底面
底面![]() ,
,![]() ,
,
所以![]() 底面
底面![]() ,所以
,所以![]() ;
;
又底面![]() 是直角梯形,
是直角梯形,![]() ,
,
所以![]() ,
,
因此![]() ,所以
,所以![]() ;
;
又![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)由(1)可得![]() 两两垂直,
两两垂直,
因此以![]() 点为坐标原点,以
点为坐标原点,以![]() 方向分别为
方向分别为![]() 轴,
轴,![]() 轴,
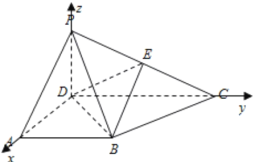
轴,![]() 轴正方向,建立如图所示的空间直角坐标系;
轴正方向,建立如图所示的空间直角坐标系;
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
由(1)可知![]() 平面
平面![]() ;所以
;所以![]() 为平面
为平面![]() 的一个法向量;
的一个法向量;
又因为![]() ,
,
所以![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则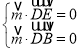 ,即
,即![]() ,令
,令![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,
,
又二面角![]() 的大小为
的大小为![]() ,
,
所以![]() ,化简整理得
,化简整理得![]() ,
,
解得![]() ,
,
因为![]() 为侧棱
为侧棱![]() 上一点,所以
上一点,所以![]() ,
,
因此![]() .
.

练习册系列答案
相关题目
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中选
人中选![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?
,你有多大把握认为心肺疾病与性别有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:  ,其中
,其中![]() .
.


