题目内容
(2014·天门模拟)在区间[0,4]内随机取两个数a,b,则使得函数f(x)=x2+ax+b2有零点的概率为________.

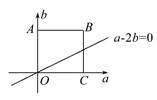
因为两个数a,b在区间[0,4]内随机取,所以以a为横坐标,b为纵坐标建立如图所示的直角坐标系,可得对应的点(a,b)在如图的正方形OABC及其内部任意取,其中A(0,4),B(4,4),C(4,0),O为坐标原点,若函数f(x)=x2+ax+b2有零点,则Δ=a2-4b2≥0,解之得a≥2b,满足条件的点(a,b)在直线a-2b=0的下方,且在正方形OABC内部的三角形,其面积为S1= ×4×2=4,因为正方形OABC的面积为S=4×4=16,所以函数f(x)=x2+ax+b2有零点的概率为P=
×4×2=4,因为正方形OABC的面积为S=4×4=16,所以函数f(x)=x2+ax+b2有零点的概率为P=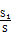 =
=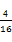 =
= .
.
 ×4×2=4,因为正方形OABC的面积为S=4×4=16,所以函数f(x)=x2+ax+b2有零点的概率为P=
×4×2=4,因为正方形OABC的面积为S=4×4=16,所以函数f(x)=x2+ax+b2有零点的概率为P=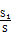 =
=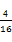 =
= .
.

练习册系列答案
相关题目
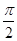
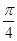
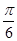
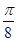
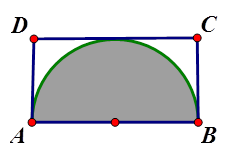
 的值.如果撒了1000个芝麻,落在圆内的芝麻总数是781颗,那么这次模拟中
的值.如果撒了1000个芝麻,落在圆内的芝麻总数是781颗,那么这次模拟中
 )的概率为( )
)的概率为( )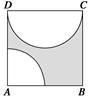
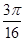
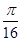
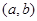 是区域
是区域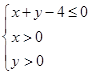 内的随机点,函数
内的随机点,函数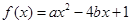 在区间
在区间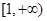 上是增函数的概率为 ( )
上是增函数的概率为 ( ) 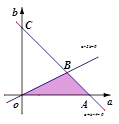
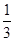

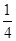
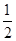
 内随机取一点,则所取的点恰好满足
内随机取一点,则所取的点恰好满足 的概率是( )
的概率是( )