题目内容
用反证法证明命题:“若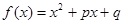 ,那么
,那么 ,
,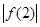 ,
,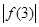 中至少有一个不小于
中至少有一个不小于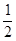 ”时,反设正确的是 ( )
”时,反设正确的是 ( )
A.假设 , ,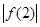 , ,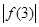 都不小于 都不小于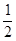 |
B.假设 , ,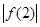 , ,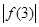 都小于 都小于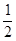 |
C.假设 , ,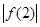 , ,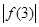 至多有两个小于 至多有两个小于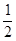 |
D.假设 , ,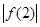 , ,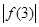 至多有一个小于 至多有一个小于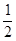 |
B
解析试题分析:根据题意,由于反证法证明命题:“若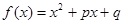 ,那么
,那么 ,
,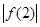 ,
,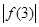 中至少有一个不小于
中至少有一个不小于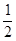 ”时,即将结论变为否定就是对命题的反设,因此可知至少有一个的否定是一个也没有,或者说假设
”时,即将结论变为否定就是对命题的反设,因此可知至少有一个的否定是一个也没有,或者说假设 ,
,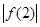 ,
,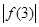 都小于
都小于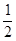 ,故答案为B.
,故答案为B.
考点:反证法
点评:主要是考查了反证法的运用,属于基础题。

练习册系列答案
相关题目
下列表述正确的是
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
| A.①②③ | B.②③④ | C.②④⑤ | D.①③⑤ |
对命题“正三角形的内切圆切于三边的中点”可类比猜想出:正四面体的内切球切于四面都为正三角形的什么位置?( )
| A.正三角形的顶点 | B.正三角形的中心 |
| C.正三角形各边的中点 | D.无法确定 |
用反证法证明某命题时,对其结论:“自然数 中恰有一个偶数”正确的反设为( )
中恰有一个偶数”正确的反设为( )
A. 都是奇数 都是奇数 |
B. 都是偶数 都是偶数 |
C. 中至少有两个偶数 中至少有两个偶数 |
D. 中至少有两个偶数或都是奇数 中至少有两个偶数或都是奇数 |
下面几种推理中是演绎推理的序号为( )
A.半径为 圆的面积 圆的面积 ,则单位圆的面积 ,则单位圆的面积 ; ; |
| B.由金、银、铜、铁可导电,猜想:金属都可导电; |
C.猜想数列 的通项公式为 的通项公式为  ; ; |
D.由平面直角坐标系中圆的方程为 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为 . . |
用演绎法证明函数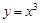 是增函数时的小前提是 ( )
是增函数时的小前提是 ( )
| A.增函数的定义 | B.函数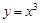 满足增函数的定义 满足增函数的定义 |
C.若 ,则 ,则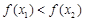 | D.若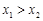 ,则 ,则 |
三段论:“①所有的中国人都坚强不屈;②玉树人是中国人;③玉树人一定坚强不屈”中,其中“大前提”和“小前提”分别是( )
| A.①② | B.①③ |
| C.②③ | D.②① |
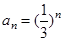 ,把数列
,把数列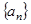 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,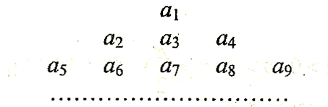
 表示第
表示第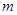 行的第
行的第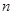 个数,则
个数,则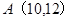 = ( )
= ( )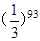

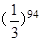
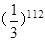
 表示第
表示第 幅图的蜂巢总数,则
幅图的蜂巢总数,则