题目内容
下列表述正确的是
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.
| A.①②③ | B.②③④ | C.②④⑤ | D.①③⑤ |
D
解析试题分析:由归纳推理,演绎推理,类比推理的定义,知,归纳推理是由部分到整体的推理;演绎推理是由一般到特殊的推理;类比推理是由特殊到特殊的推理.正确,即选D.
考点:归纳推理,演绎推理,类比推理。
点评:简单题,关键是理解归纳推理,演绎推理,类比推理。的概念。

练习册系列答案
相关题目
已知集合A={3m+2n|m>n且m,n∈N},若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…,依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )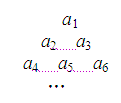
| A.247 | B.735 |
| C.733 | D.731 |
已知数列{an}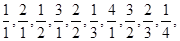 …,依它的10项的规律,则a99+a100的值为( )
…,依它的10项的规律,则a99+a100的值为( )
A.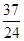 | B. | C.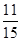 | D.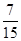 |
若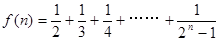 ,则
,则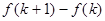 等于( )
等于( )
A.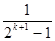 | B.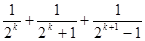 |
C.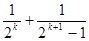 | D.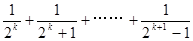 |
观察式子:1+ <
< ,1+
,1+ +
+ <
< ,1+
,1+ +
+ +
+ <
< , ,则可归纳出一般式子为( )
, ,则可归纳出一般式子为( )
A.1+ + + + + + + < < (n≥2) (n≥2) | B.1+ + + + + + + < < (n≥2) (n≥2) |
C.1+ + + + + + + < < (n≥2) (n≥2) | D.1+ + + + + + + < < (n≥2) (n≥2) |
用反证法证明命题:“若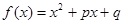 ,那么
,那么 ,
,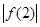 ,
,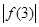 中至少有一个不小于
中至少有一个不小于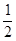 ”时,反设正确的是 ( )
”时,反设正确的是 ( )
A.假设 , ,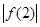 , ,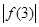 都不小于 都不小于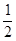 |
B.假设 , ,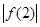 , ,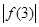 都小于 都小于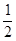 |
C.假设 , ,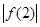 , ,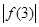 至多有两个小于 至多有两个小于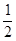 |
D.假设 , ,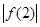 , ,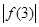 至多有一个小于 至多有一个小于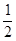 |
在用数学归纳法证明 时,在验证当
时,在验证当 时,等式左边为( )
时,等式左边为( )
| A.1 | B. | C. | D. |
已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N*,f(n)都能被m整除,则m的最大值为( )
| A.18 | B.36 | C.48 | D.54 |
 ,则
,则 .
.