题目内容

13．已知（2x-$\frac{a}{x}$）8展开式中常数项为1120，其中a是正数，则展开式中各项系数和是1．

分析 由题意写出常数项，由题意可得a值，令x=1计算式子的值即为所求．

解答 解：由题意可得常数项为：${C}_{8}^{4}$（2x）4（-$\frac{a}{x}$）4=1120a4，
∴a4=1，∵a是正数，∴a=1，
令x=1可得（2x-$\frac{a}{x}$）8=（2-1）8=1，
∴展开式中各项系数和为：1
故答案为：1

点评 本题考查二项式系数的性质，属基础题．

练习册系列答案
相关题目
3．已知Sn是等差数列{an}的前n项和，S3=6，an-2+an=16，若Sn=50，则n的值为10．
4．已知C${\;}_{2}^{2}$+C${\;}_{3}^{2}$+…+C${\;}_{n}^{2}$=C${\;}_{8}^{3}$（n∈N*）．
（1）求n的值；
（2）求二项式（$\sqrt{x}$-$\frac{2}{\root{3}{x}}$）n展开式的一次项．
1．关于x的不等式x2-2x+3＞0解集为（　　）
A．（-1，3）B．∅C．RD．（-∞，-1）∪（3，+∞）
8．已知△ABC中，a：b：c=2：$\sqrt{6}$：（$\sqrt{3}$+1），求△ABC各角的度数．
18．已知直线L1：（3+m）x+4y=5-3m与直线L2：2x+（6+m）y=8垂直，则m的值为（　　）
A．5B．-5C．3D．-4
5．已知数列{an}是以a为首项，q为公比的等比数列，Sn为它的前n项和．
（1）当S1，S3，S4成等差数列时，求q的值；
（2）若bn=anan+1（n∈N+），试求数列{bn}的前n项和Sn的公式．
2．设向量$\overrightarrow{a}$=（λ+2，λ2-$\sqrt{3}$cosα），$\overrightarrow{b}$=（m，$\frac{m+sinα}{2}$），其中λ，m，α为实数．
（1）若λ=m=0，$\overrightarrow{a}$•$\overrightarrow{b}$=cos2α+$\frac{1}{8}$，求tanα；
（2）若$\overrightarrow{a}$=2$\overrightarrow{b}$，求$\frac{λ}{m}$的取值范围．
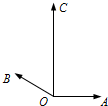3．如图，平面内有三个向量$\overrightarrow{OA}，\;\overrightarrow{OB}，\;\overrightarrow{OC}$，其中$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为150°，$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为90°，且$|{\overrightarrow{OA}}|=|{\overrightarrow{OB}}|=1$，$|{\overrightarrow{OC}}|=2$，若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}\;（λ，μ∈R）$，则λ+μ=（　　）
A．2B．4C．$\sqrt{3}$+2D．2$\sqrt{3}$+4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网