题目内容
【题目】如图,四边形ABCD外接于圆,AC是圆周角∠BAD的角平分线,过点C的切线与AD延长线交于点E,AC交BD于点F. 
(1)求证:BD∥CE;
(2)若AB是圆的直径,AB=4,DE=1,求AD的长度.
【答案】
(1)证明:∵AC是圆周角∠BAD的角平分线,∴∠EAC=∠BAC,
又∵CE是圆的切线,∴∠ECD=∠EAC,∴∠ECD=∠BAC,
又∵∠BAC=∠BDC,∴∠ECD=∠BDC,
∴BD∥CE
(2)解:由(1)知∠ECD=∠BAC,∠CED=∠ADB,
∵AB是圆的直径,∴∠ACB=∠ADB=90°,∴∠CED=∠ACB=90°,
∴ ![]() ,∴
,∴ ![]() ,
,
∵∠EAC=∠DBC,由(1)知∠EAC=∠BDC,∴∠DBC=∠BDC,∴DC=BC,
∴ ![]() ,则BC2=ABDE=4,∴BC=2
,则BC2=ABDE=4,∴BC=2
∴在Rt△ABC中, ![]() ,∴∠BAC=30°,∴∠BAD=60°,
,∴∠BAC=30°,∴∠BAD=60°,
∴在Rt△ABD中,∠ABD=30°,
所以 ![]()
【解析】(1)根据圆的切线性质结合角平分线的性质即可证明BD∥CE;(2)若AB是圆的直径,AB=4,DE=1,根据三角形相似的性质即可求AD的长度.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: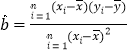 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API | [0,100] | (100,200] | (200,300] | >300 |
空气质量 | 优良 | 轻污染 | 中度污染 | 重度污染 |
天数 | 17 | 45 | 18 | 20 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为![]() .当
.当![]() 时,企业没有造成经济损失;当
时,企业没有造成经济损失;当![]() 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当![]() 时造成的经济损失为
时造成的经济损失为![]() ,当
,当![]() 时,造成的经济损失
时,造成的经济损失![]() );当
);当![]() 时造成的经济损失为2000元;
时造成的经济损失为2000元;
(1)试写出![]() 的表达式;
的表达式;
(2)若本次抽取的样本数据有30天是在供暖季,其中有12天为重度污染,完成下面2×2列联表,并判断能否有99%的把握认为该市本年空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
![]()
P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |