题目内容
(本小题满分12分)点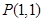 为椭圆
为椭圆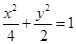 内的一定点,过P点引一直线,与椭圆相交于
内的一定点,过P点引一直线,与椭圆相交于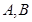 两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。
两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。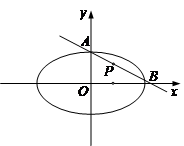
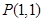 为椭圆
为椭圆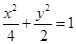 内的一定点,过P点引一直线,与椭圆相交于
内的一定点,过P点引一直线,与椭圆相交于 两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。
两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。
 。
。试题分析:由于A,B两点是直线与椭圆的交点,故他们应满足椭圆方程,设出它们的坐标,然后根据它们的中点为M,可将坐标间的关系转化为求直线l的斜率,然后再由点斜式求出直线方程.利用两点距离公式得到弦的长度的求解。
解:设直线与椭圆交于
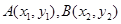 ,则
,则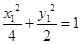 …①且
…①且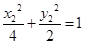 …②
…②②-①得
 ,即
,即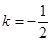 ,
,∴所求直线方程为:
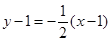 ,即
,即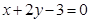 。
。将其代入椭圆方程整理得,
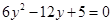 ,根据弦长公式有
,根据弦长公式有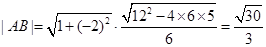 。
。点评:解决该试题的关键是求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件,用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直或经过原点的直线,故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.

练习册系列答案
相关题目
 (a>0,b>0)的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
(a>0,b>0)的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )


 -1
-1
 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则m的值为 ( )
轴上,长轴长是短轴长的两倍,则m的值为 ( )



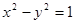 的左右焦点,点P在C上,
的左右焦点,点P在C上,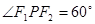 ,则
,则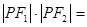 ( )
( ) 与圆
与圆 在第一象限的交点,
在第一象限的交点, 分别是双曲线的左右焦点,且
分别是双曲线的左右焦点,且 则双曲线的离心率为( )
则双曲线的离心率为( )
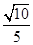


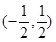
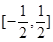

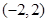
 与抛物线
与抛物线 的一个交点为M,
的一个交点为M, 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为 

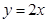 ,焦距为
,焦距为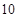 ,这双曲线的方程为___
,这双曲线的方程为___  内有一动点
内有一动点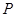 ,已知
,已知 ,且满足
,且满足 ,求
,求