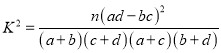题目内容
【题目】设函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的条件下,是否存在实常数![]() 和
和![]() ,使得
,使得![]() 和
和![]() ?若存在,求出
?若存在,求出![]() 和
和![]() 的值.若不存在,说明理由;
的值.若不存在,说明理由;
(Ⅲ)设![]() 有两个零点
有两个零点![]() ,且
,且![]() 成等差数列,试探究
成等差数列,试探究![]() 值的符号.
值的符号.
【答案】(1)极小值为0(2)k=2,m= -1(3)![]()
【解析】试题分析:(Ⅰ)首先由![]() ,得到关于
,得到关于![]() 的两个方程,从而求出
的两个方程,从而求出![]() ,这样就可得到
,这样就可得到![]() 的表达式,根据它的特点可想到用导数的方法求出
的表达式,根据它的特点可想到用导数的方法求出![]() 的极小值; (Ⅱ)由(Ⅰ)中所求的
的极小值; (Ⅱ)由(Ⅰ)中所求的![]() 和
和![]() ,易得到它们有一个公共的点
,易得到它们有一个公共的点![]() ,且
,且![]() 和
和![]() 在这个点处有相同的切线
在这个点处有相同的切线![]() ,这样就可将问题转化为证明
,这样就可将问题转化为证明![]() 和
和![]() 分别在这条切线
分别在这条切线![]() 的上方和下方,两线的上下方可转化为函数与0的大小,即证
的上方和下方,两线的上下方可转化为函数与0的大小,即证![]() 和
和![]() 成立,从而得到
成立,从而得到![]() 和
和![]() 的值; (Ⅲ)由已知易得
的值; (Ⅲ)由已知易得![]() ,由零点的意义,可得到关于
,由零点的意义,可得到关于![]() 两个方程,根据结构特征将两式相减,得到关于
两个方程,根据结构特征将两式相减,得到关于![]() 的关系式
的关系式![]() ,又对
,又对![]() 求导,进而得到
求导,进而得到![]() ,结合上面关系可化简得:
,结合上面关系可化简得: 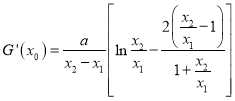 ,针对特征将
,针对特征将![]() 当作一个整体,可转化为关于
当作一个整体,可转化为关于![]() 的函数
的函数![]() ,对其求导分析得,
,对其求导分析得, ![]() 恒成立.
恒成立.
试题解析:解:(Ⅰ)由![]() ,得
,得![]() ,解得
,解得![]() 2分
2分
则![]() =
= ![]() ,
,
利用导数方法可得![]() 的极小值为
的极小值为![]() 5分
5分
(Ⅱ)因![]() 与
与![]() 有一个公共点
有一个公共点![]() ,而函数
,而函数![]() 在点
在点![]() 的切线方程为
的切线方程为![]() ,
,
下面验证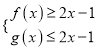 都成立即可 7分
都成立即可 7分
由![]() ,得
,得![]() ,知
,知![]() 恒成立 8分
恒成立 8分
设![]() ,即
,即![]() ,易知其在
,易知其在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以![]() 的最大值为
的最大值为![]() ,所以
,所以![]() 恒成立.
恒成立.
故存在这样的k和m,且![]() 10分
10分
(Ⅲ)![]() 的符号为正. 理由为:因为
的符号为正. 理由为:因为![]() 有两个零点
有两个零点![]() ,则有
,则有
![]() ,两式相减得
,两式相减得![]() 12分
12分
即![]() ,于是
,于是![]()
![]()
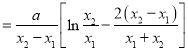
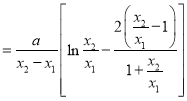 14分
14分
①当![]() 时,令
时,令![]() ,则
,则![]() ,且
,且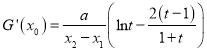 .
.
设![]() ,则
,则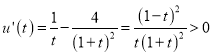 ,则
,则![]() 在
在![]() 上为增函数.而
上为增函数.而![]() ,所以
,所以![]() ,即
,即![]() . 又因为
. 又因为![]() ,所以
,所以![]() .
.
②当![]() 时,同理可得:
时,同理可得: ![]() .
.
综上所述: ![]() 的符号为正 16分
的符号为正 16分

练习册系列答案
相关题目