题目内容
如图,三棱柱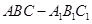 中,侧棱
中,侧棱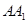 垂直底面
垂直底面 ,底面三角形
,底面三角形 是正三角形,
是正三角形, 是
是 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )
A.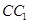 与 与 是异面直线 是异面直线 |
B. 平面 平面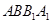 |
C.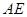 , ,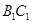 为异面直线,且 为异面直线,且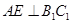 |
D.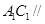 平面 平面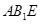 |
C
解析试题分析:C.三棱柱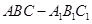 中,底面是互相平行的,又E在边BC上,所以
中,底面是互相平行的,又E在边BC上,所以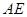 ,
,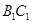 无交点,故是异面直线,又底面三角形
无交点,故是异面直线,又底面三角形 是正三角形,
是正三角形, 是
是 中点,所以AE⊥BC,BC//B1C1
中点,所以AE⊥BC,BC//B1C1  AE⊥B1C1,显然C正确;
AE⊥B1C1,显然C正确;
A. 是
是 中点,显然
中点,显然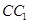 与
与 是共面的直线;此选项错误;
是共面的直线;此选项错误;
B.若 平面
平面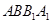 ,则AC⊥AB,而∠CAB=60°,显然是矛盾的,此选项错误;
,则AC⊥AB,而∠CAB=60°,显然是矛盾的,此选项错误;
考点:线面位置关系的判断.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
设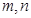 是不同的直线,
是不同的直线,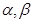 是不同的平面,下列命题中正确的是 ( )
是不同的平面,下列命题中正确的是 ( )
A.若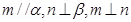 ,则 ,则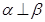 |
B.若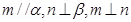 ,则 ,则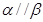 |
C.若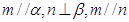 ,则 ,则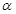 ⊥ ⊥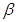 |
D.若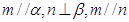 ,则 ,则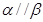 |
三棱柱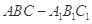 中,侧棱
中,侧棱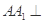 底面
底面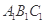 ,底面三角形
,底面三角形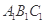 是正三角形,
是正三角形, 是
是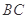 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )
A.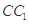 与 与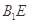 是异面直线 是异面直线 |
B.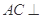 平面 平面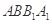 |
C. 、 、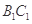 为异面直线,且 为异面直线,且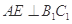 |
D.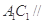 平面 平面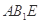 |
已知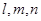 是三条不同的直线,
是三条不同的直线,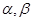 是两个不同的平面,下列命题为真命题的是( )
是两个不同的平面,下列命题为真命题的是( )
A.若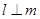 , , , , , ,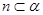 ,则 ,则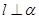 |
B.若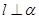 , ,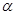 ∥ ∥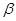 , ,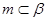 ,则 ,则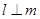 |
C.若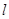 ∥ ∥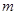 , , ,则 ,则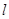 ∥ ∥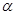 |
D.若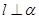 , ,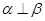 , ,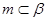 ,则 ,则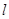 ∥ ∥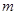 |
如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )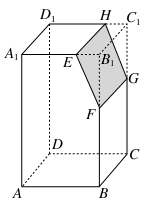
| A.EH∥FG |
| B.四边形EFGH是矩形 |
| C.Ω是棱柱 |
| D.Ω是棱台 |
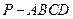 的底面
的底面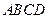 是边长为1的菱形,
是边长为1的菱形,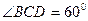 ,
,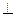 底面ABCD,
底面ABCD,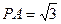 。
。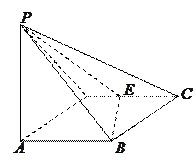
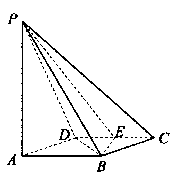
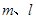 ,平面
,平面 ,且
,且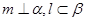 ,下列命题中正确命题的个数是
,下列命题中正确命题的个数是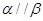 ,则
,则 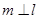 ②若
②若 ,则
,则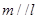
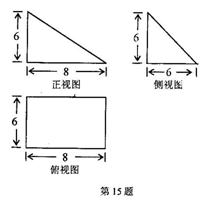
 图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:
图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位: )
) 图中连结
图中连结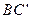 ,证明:
,证明: