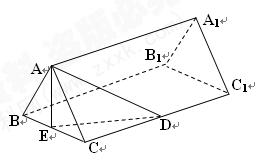
题目内容
三棱柱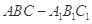 中,侧棱
中,侧棱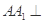 底面
底面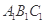 ,底面三角形
,底面三角形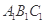 是正三角形,
是正三角形, 是
是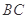 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )
A.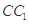 与 与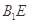 是异面直线 是异面直线 |
B.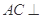 平面 平面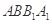 |
C. 、 、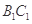 为异面直线,且 为异面直线,且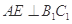 |
D.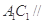 平面 平面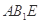 |
C
解析试题分析:作出草图:知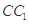 与
与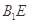 都在平面BCC1B1内,所以不是异面直线;对于B,取AB的中点为F,联结CF,由于底面三角形
都在平面BCC1B1内,所以不是异面直线;对于B,取AB的中点为F,联结CF,由于底面三角形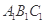 是正三角形,所以CF
是正三角形,所以CF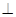 AB,又因为侧棱
AB,又因为侧棱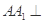 底面
底面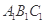 ,所以
,所以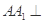 底面ABC,从而有CF
底面ABC,从而有CF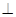 AA1,所以有CF
AA1,所以有CF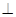 平面
平面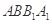 ,而过一点有且只有一条直线和一个平面垂直,故AC与平面
,而过一点有且只有一条直线和一个平面垂直,故AC与平面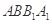 不可能垂直;同理可知AE
不可能垂直;同理可知AE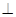 平面BCC1B1,所以
平面BCC1B1,所以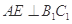 ,显然
,显然 、
、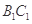 为异面直线,故选C.
为异面直线,故选C.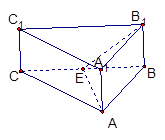
考点:空间中直线与平面的位置关系.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
如图,三棱柱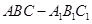 中,侧棱
中,侧棱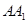 垂直底面
垂直底面 ,底面三角形
,底面三角形 是正三角形,
是正三角形, 是
是 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )
A.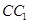 与 与 是异面直线 是异面直线 |
B. 平面 平面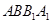 |
C.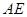 , ,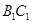 为异面直线,且 为异面直线,且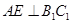 |
D.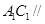 平面 平面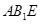 |
直三棱柱 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,则
,则 与
与 所成的角的余弦值为( ).
所成的角的余弦值为( ).
A. | B. | C. | D. |
已知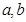 是两条不同的直线,
是两条不同的直线,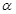 是一个平面,则下列说法正确的是( )
是一个平面,则下列说法正确的是( )
A.若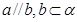 ,则 ,则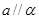 | B.若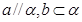 ,则 ,则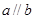 |
C.若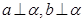 ,则 ,则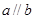 | D.若 ,则 ,则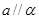 |
设 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知 为异面直线,
为异面直线,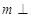 平面
平面 ,
, 平面
平面 .平面α与β外的直线
.平面α与β外的直线 满足
满足 ,则( )
,则( )
A. ,且 ,且 | B. ,且 ,且 |
C. 与 与 相交,且交线垂直于 相交,且交线垂直于 | D. 与 与 相交,且交线平行于 相交,且交线平行于 |
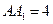 ,
,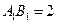 ,俯视图是一个正三角形.
,俯视图是一个正三角形.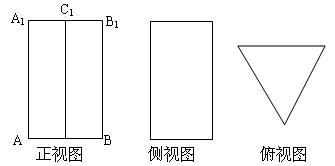
 )
) 的底面边长是
的底面边长是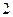 ,
,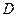 、E是
、E是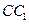 、BC的中点,AE=DE
、BC的中点,AE=DE