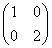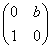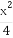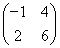题目内容
对任意实数x,矩阵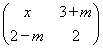
总存在特征向量,求m的取值范围.
-3≤m≤2
【解析】由条件得特征多项式λ2-(x+2)λ+2x+(m+3)(m-2),
则λ2-(x+2)λ+2x+(m+3)(m-2)=0有实数根,
得:Δ1=(x+2)2-4(2x+m2+m-6)≥0对任意实数x恒成立,
所以Δ2=16+4(4m2+4m-28)≤0,
解之得: m的取值范围是-3≤m≤2.
练习册系列答案
名校课堂系列答案
相关题目
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
射击环数 | 频数 | 频率 |
7 | 10 | 0.1 |
8 | 10 | 0.1 |
9 | x | 0.45 |
10 | 35 | y |
合计 | 100 | 1 |
乙运动员
射击环数 | 频数 | 频率 |
7 | 8 | 0.1 |
8 | 12 | 0.15 |
9 | z |
|
10 |
| 0.35 |
合计 | 80 | 1 |
若将频率视为概率,回答下列问题:
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).
