题目内容
17.已知关于x的不等式|x+a|<b的解集为{x|2<x<4}(Ⅰ)求实数a,b的值;
(Ⅱ)求$\sqrt{at+12}$+$\sqrt{bt}$的最大值.
分析 (Ⅰ)由不等式的解集可得ab的方程组,解方程组可得;
(Ⅱ)原式=$\sqrt{-3t+12}$+$\sqrt{t}$=$\sqrt{3}$$\sqrt{4-t}$+$\sqrt{t}$,由柯西不等式可得最大值.
解答 解:(Ⅰ)关于x的不等式|x+a|<b可化为-b-a<x<b-a,
又∵原不等式的解集为{x|2<x<4},
∴$\left\{\begin{array}{l}{-b-a=2}\\{b-a=4}\end{array}\right.$,解方程组可得$\left\{\begin{array}{l}{a=-3}\\{b=1}\end{array}\right.$;
(Ⅱ)由(Ⅰ)可得$\sqrt{at+12}$+$\sqrt{bt}$=$\sqrt{-3t+12}$+$\sqrt{t}$
=$\sqrt{3}$$\sqrt{4-t}$+$\sqrt{t}$≤$\sqrt{[(\sqrt{3})^{2}+{1}^{2}][(\sqrt{4-t})^{2}+(\sqrt{t})^{2}]}$
=2$\sqrt{4-t+t}$=4,
当且仅当$\frac{\sqrt{4-t}}{\sqrt{3}}$=$\frac{\sqrt{t}}{1}$即t=1时取等号,
∴所求最大值为4
点评 本题考查不等关系与不等式,涉及柯西不等式求最值,属基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
| A. | 134石 | B. | 169石 | C. | 338石 | D. | 1365石 |
12.设f(x)=lnx,0<a<b,若p=f($\sqrt{ab}$),q=f($\frac{a+b}{2}$),r=$\frac{1}{2}$(f(a)+f(b)),则下列关系式中正确的是( )
| A. | q=r<p | B. | p=r<q | C. | q=r>p | D. | p=r>q |
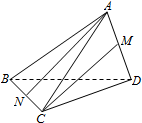 如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$.
如图,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是$\frac{7}{8}$. 如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.