题目内容
8.解不等式x+|2x+3|≥2.分析 思路1(公式法):利用|f(x)|≥g(x)?f(x)≥g(x),或f(x)≤-g(x);
思路2(零点分段法):对x的值分“x≥$-\frac{3}{2}$”“x<$-\frac{3}{2}$”进行讨论求解.
解答 解法1:x+|2x+3|≥2变形为|2x+3|≥2-x,
得2x+3≥2-x,或2x+3≤-(2-x),
即x≥$-\frac{1}{3}$,或x≤-5,
即原不等式的解集为{x|x≥$-\frac{1}{3}$,或x≤-5}.
解法2:令|2x+3|=0,得x=$-\frac{3}{2}$.
①当x≥$-\frac{3}{2}$时,原不等式化为x+(2x+3)≥2,即x≥$-\frac{1}{3}$,
所以x≥$-\frac{1}{3}$;
②x<$-\frac{3}{2}$时,原不等式化为x-(2x+3)≥2,即x≤-5,
所以x≤-5.
综上,原不等式的解集为{x|x≥$-\frac{1}{3}$,或x≤-5}.
点评 本题考查了含绝对值不等式的解法.本解答给出的两种方法是常见的方法,不管用哪种方法,其目的是去绝对值符号.若含有一个绝对值符号,利用公式法要快捷一些,其套路为:|f(x)|≥g(x)?f(x)≥g(x),或f(x)≤-g(x);|f(x)|≤g(x)?-g(x)≤f(x)≤g(x).可简记为:大于号取两边,小于号取中间.使用零点分段法时,应注意:同一类中取交集,类与类之间取并集.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表
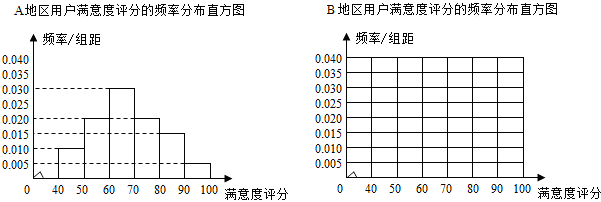
B地区用户满意度评分的频数分布表
(1)做出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可)
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:
估计哪个地区用户的满意度等级为不满意的概率大?说明理由.

B地区用户满意度评分的频数分布表
| 满意度评分分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 2 | 8 | 14 | 10 | 6 |
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个不等级:
| 满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
| 满意度等级 | 不满意 | 满意 | 非常满意 |
18.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{3}+2π$ | B. | $\frac{13π}{6}$ | C. | $\frac{7π}{3}$ | D. | $\frac{5π}{2}$ |
 某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米,以l2,l1在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{{x}^{2}+b}$(其中a,b为常数)模型.
某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米,以l2,l1在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{{x}^{2}+b}$(其中a,b为常数)模型. 程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )
程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )