题目内容
11.已知数列{an}满足nan=(n-1)an-1(n≥2,n∈N*),a1=1,求an.分析 通过对nan=(n-1)an-1变形可知$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n}$,从而$\frac{{a}_{n-1}}{{a}_{n-2}}$=$\frac{n-2}{n-1}$、…、$\frac{{a}_{2}}{{a}_{1}}$=$\frac{1}{2}$,利用累乘法计算即得结论.
解答 解:∵nan=(n-1)an-1(n≥2,n∈N*),
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n}$,
∴$\frac{{a}_{n-1}}{{a}_{n-2}}$=$\frac{n-2}{n-1}$,
…
$\frac{{a}_{2}}{{a}_{1}}$=$\frac{1}{2}$,
累乘得:$\frac{{a}_{n}}{{a}_{1}}$=$\frac{1}{n}$,
又∵a1=1,
∴an=$\frac{1}{n}$.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
20.钝角三角形ABC的面积为3$\sqrt{3}$,BC=3,AC=4,则AB=( )
| A. | $\sqrt{13}$ | B. | $\sqrt{37}$ | C. | 6 | D. | 7 |
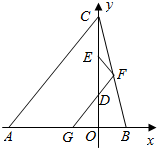 如图,△ABC的三个顶点坐标分别为A(-6,0),B(2,0),C(0,6),D,E分别是高CO的两个三等分点,过D,作直线FG∥AC,分别交AB和BC于G,F,连接EF.
如图,△ABC的三个顶点坐标分别为A(-6,0),B(2,0),C(0,6),D,E分别是高CO的两个三等分点,过D,作直线FG∥AC,分别交AB和BC于G,F,连接EF.