题目内容
16.已知函数y=-2sinx.(1)用“五点法”作出该函数在区间[0,2π]的图象;
(2)求该函数的最大值及取最大值时自变量x的集合;
(3)写出该函数的单调递增区间,及单调递减区间.
分析 (1)利用“五点法”,即可作出该函数在区间[0,2π]的图象;
(2)根据正弦函数的有界性即可求该函数的最大值及取最大值时自变量x的集合;
(3)结合三角函数的单调性即可写出该函数的单调递增区间,及单调递减区间.
解答  解:(1)
解:(1)
| x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sinx | 0 | 1 | 0 | -1 | 0 |
| y=-2sinx | 0 | -2 | 0 | 2 | 0 |
(2)当sinx=1时,函数取得最小值y=-2,此时x=2kπ+$\frac{π}{2}$,k∈Z,对应的集合为{x|x=2kπ+$\frac{π}{2}$,k∈Z},
当sinx=-1时,函数取得最大值y=2,此时x=2kπ-$\frac{π}{2}$,k∈Z,对应的集合为{x|x=2kπ-$\frac{π}{2}$,k∈Z},
(2)当2kπ-$\frac{π}{2}$≤x≤2kπ+$\frac{π}{2}$,k∈Z时,函数单调递减,
当2kπ+$\frac{π}{2}$≤x≤2kπ+$\frac{3π}{2}$,k∈Z时,函数单调递增,
故单调递增区间为为[2kπ+$\frac{π}{2}$,2kπ+$\frac{3π}{2}$],k∈Z,
单调递减区间为[2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$],k∈Z.
点评 本题主要考查三角函数的图象和性质,根据正弦函数的图象是解决本题的关键.

练习册系列答案
相关题目
11.过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若$\overrightarrow{FB}=2\overrightarrow{BC}$,则双曲线的离心率是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | 5 | D. | $\sqrt{10}$ |
8.如何由y=x2的图象平移得到y=x2-2x的图象( )
| A. | 向右平移一个单位,再向上平移一个单位 | |
| B. | 向左平移一个单位,再向上平移一个单位 | |
| C. | 向右平移一个单位,再向下平移一个单位 | |
| D. | 向左平移一个单位,再向下平移一个单位 |
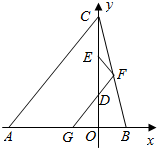 如图,△ABC的三个顶点坐标分别为A(-6,0),B(2,0),C(0,6),D,E分别是高CO的两个三等分点,过D,作直线FG∥AC,分别交AB和BC于G,F,连接EF.
如图,△ABC的三个顶点坐标分别为A(-6,0),B(2,0),C(0,6),D,E分别是高CO的两个三等分点,过D,作直线FG∥AC,分别交AB和BC于G,F,连接EF.