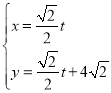题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,若直线
时,若直线![]() 是曲线
是曲线![]() 的切线,求
的切线,求![]() 的最大值;
的最大值;
(2)设![]() ,函数
,函数![]() 有两个不同的零点,求
有两个不同的零点,求![]() 的最大整数值.(参考数据
的最大整数值.(参考数据![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用导数的几何意义可得![]() ,因此
,因此![]() ,
,![]() 利用导数研究其单调性,即可求出
利用导数研究其单调性,即可求出![]() 的最大值,即求出
的最大值,即求出![]() 的最大值.
的最大值.
(2)根据题意,关于![]() 的方程
的方程![]() 有两个不同的解,设
有两个不同的解,设![]() 利用导数得到存在
利用导数得到存在![]() 使得
使得![]() .则要使得关于
.则要使得关于![]() 的方程
的方程![]() 有两个不同的解,则
有两个不同的解,则![]() ,当
,当![]() 时,设
时,设![]() 经验证
经验证![]() 有两个不同的零点,即可证明.
有两个不同的零点,即可证明.
解:(1)设直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又因为点![]() 在切线
在切线![]() 上,所以
上,所以![]() .所以
.所以![]()
![]() .因此
.因此![]()
设![]() ,则
,则![]()
令![]() 得,
得,![]() ;令
;令![]() 得,
得,![]() .
.
![]() 在
在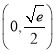 上单调递增,在
上单调递增,在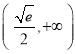 上单调递减.
上单调递减.
![]() 的最大值为
的最大值为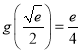 .则
.则![]() 的最大值为
的最大值为![]() .
.
(2)函数![]() 有两个不同的零点,
有两个不同的零点,
等价于方程![]() 有两个不相等的实根.
有两个不相等的实根.
设![]() ,则等价于方程
,则等价于方程![]() 有两个不同的解,
有两个不同的解,
即关于![]() 的方程
的方程![]() 有两个不同的解,设
有两个不同的解,设![]() ,
,
则![]() .设
.设![]() ,由
,由![]() 可知
可知![]()
![]() 在
在![]() 上单调递减,又
上单调递减,又![]()
![]() 存在
存在![]() 使得
使得![]() ,即
,即![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递增;当
单调递增;当![]() 时
时
![]() ,
,![]() ,函数
,函数![]() 单调递减.所以函数
单调递减.所以函数![]() 的极大值为
的极大值为
![]() .
.
要使得关于![]() 的方程
的方程![]() 有两个不同的解,则
有两个不同的解,则![]() .
.
当![]() 时,设
时,设![]() ,则
,则![]()
可知![]() 在
在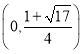 上单调递增,在
上单调递增,在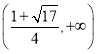 上单调递减,
上单调递减,
又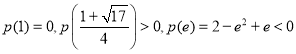 p(1)=0
p(1)=0
所以![]() 有两个不同的零点,符合题意,所以
有两个不同的零点,符合题意,所以![]() 的最大整数值为
的最大整数值为![]() .
.

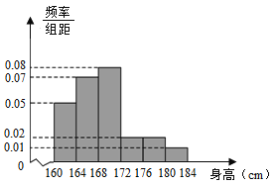
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
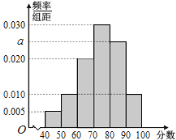
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:
内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:
甲套设备的样本的频率分布直方图
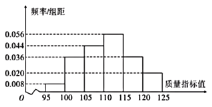
乙套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 1 | 6 | 19 | 18 | 5 | 1 |
(1)根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: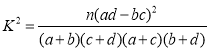 ,其中
,其中![]()