题目内容
【题目】如图，在四棱锥
中，
平面
，点
为
中点，底面为梯形，
，
，
.
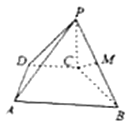
（1）证明：
平面
；
（2）若四棱锥的体积为4，求点到平面的距离.
【答案】（1）详见解析；（2）
.
【解析】
（1）取
中点
，连接
，
，根据平行四边形的性质，证得
，再利用线面平行的判定定理，即可证得
平面
.
（2）设
，利用四棱锥
的体积，求得
，又由平面知，点
到平面的距离等于点
到平面的距离,过作
，证得
平面，即可求得答案。
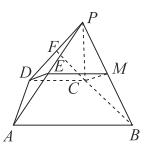
（1）如图所示，取中点，连接，，
∵是
中点，∴
，
，
又
，
，∴
，
，
∴四边形
为平行四边形，∴.
∵
平面，
平面，∴平面.
（2）设，则
，
，
由
是直角梯形，
平面知，
则四棱锥的体积为
，解得，
由平面知，点到平面的距离等于点到平面的距离,
过作，垂足为
，
由平面，得
，
又
，∴
平面
，
∵
平面，∴
，∴平面.
由
，
知
，
∴到平面的距离为.
练习册系列答案
相关题目
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动，为了解小朋友坚持打卡的情况，对该幼儿园所有小朋友进行了调查，调查结果如下表：
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
（1）根据上表数据，求该幼儿园男生平均打卡的天数；
（2）若从打卡21天的小朋友中任选2人交流心得，求选到男生和女生各1人的概率.
