题目内容
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() :
:![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,
两点,![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上,当
上,当![]() 时,
时,![]() .
.
(1)求椭圆方程;
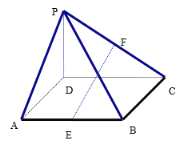
(2)试探究四边形![]() 的面积是否为定值,若是,求出此定值;若不是,请说明理由.
的面积是否为定值,若是,求出此定值;若不是,请说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)根据点差法得![]() ,解得M坐标,代入椭圆方程,与离心率联立方程组解得
,解得M坐标,代入椭圆方程,与离心率联立方程组解得![]() (2)联立直线方程与椭圆方程,利用韦达定理与弦长公式、面积公式得四边形
(2)联立直线方程与椭圆方程,利用韦达定理与弦长公式、面积公式得四边形![]() 的面积.
的面积.
解:(1)由![]() ,
,![]() ,故椭圆方程可化为
,故椭圆方程可化为![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
两式相减整理得![]() ,
,
当![]() 时,
时,![]() ,
,
解得![]() ,
,
将![]() 与
与![]() 联立,
联立,
解得![]() 中点坐标为
中点坐标为![]() ,
,
故![]() 代入椭圆
代入椭圆![]() 方程,
方程,
整理得![]() ,
,
解得![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() 中点为
中点为![]() ,
,![]() ,
,![]() ,
,
把![]() 代入椭圆
代入椭圆![]() ,
,
整理得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
设![]() ,
,
则![]() ,
,![]() ,
,
代入椭圆![]() ,得
,得![]() ,
,
![]() .
.
①当![]() 时,设
时,设![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() .
.
![]()
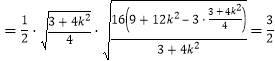 .
.
②当![]() 时,
时,![]() 的面积为
的面积为![]() ,
,
故![]() 面积为定值
面积为定值![]() .
.
因为![]() ,
,
所以四边形![]() 面积为定值3.
面积为定值3.

 名校课堂系列答案
名校课堂系列答案【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了人口规模相当的![]() 个城市采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价:
个城市采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价: ![]() (单位:元/月)和购买总人数
(单位:元/月)和购买总人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
定价x(元/月) | 20 | 30 | 50 | 60 |
年轻人(40岁以下) | 10 | 15 | 7 | 8 |
中老年人(40岁以及40岁以上) | 20 | 15 | 3 | 2 |
购买总人数y(万人) | 30 | 30 | 10 | 10 |
(Ⅰ)根据表中的数据,请用线性回归模型拟合![]() 与
与![]() 的关系,求出
的关系,求出![]() 关于
关于![]() 的回归方程;并估计
的回归方程;并估计![]() 元/月的流量包将有多少人购买?
元/月的流量包将有多少人购买?
(Ⅱ)若把![]() 元/月以下(不包括
元/月以下(不包括![]() 元)的流量包称为低价流量包,
元)的流量包称为低价流量包,![]() 元以上(包括
元以上(包括![]() 元)的流量包称为高价流量包,试运用独立性检验知识,填写下面列联表,并通过计算说明是否能在犯错误的概率不超过
元)的流量包称为高价流量包,试运用独立性检验知识,填写下面列联表,并通过计算说明是否能在犯错误的概率不超过![]() 的前提下,认为购买人的年龄大小与流量包价格高低有关?
的前提下,认为购买人的年龄大小与流量包价格高低有关?
定价x(元/月) | 小于50元 | 大于或等于50元 | 总计 |
年轻人(40岁以下) | |||
中老年人(40岁以及40岁以上) | |||
总计 |
参考公式:其中![]()
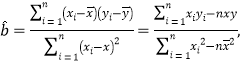
![]()
![]() 其中
其中![]()
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |