题目内容
【题目】已知函数![]() ,方程
,方程![]() 有3个不同的解
有3个不同的解![]() ,现给出下述结论:①
,现给出下述结论:①![]() ;②
;②![]() ;③
;③![]() 的极小值
的极小值![]() .则其中正确的结论的有( )
.则其中正确的结论的有( )
A.①③B.①②③C.②③D.②
【答案】C
【解析】
首先对函数求导,进一步求函数的二阶导,对二阶导的符号进行判断,得出一阶导的符号,之后对函数图象的走向以及对应的变化趋势,从而判断出导数的导函数的零点、函数的零点以及函数极小值所满足的特征,从而判断出真命题的个数得到结果.
由![]() ,
,
所以![]() 在
在![]() 递减,
递减,![]() 递增,
递增,
当![]() 时,
时,![]() ,
,
此时![]() 为增函数,方程
为增函数,方程![]() 不会有三个解,此时不符合题意,即①错误.
不会有三个解,此时不符合题意,即①错误.
若![]() 时,
时,![]() ,又
,又![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
所以![]() 有两个零点
有两个零点![]() ,不妨
,不妨![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因为![]() 时,
时,![]() ;
;![]() ;
;![]() 时,
时,![]() ,
,
所以此时![]() 有三个零点,即为
有三个零点,即为![]() ,不妨设
,不妨设![]() ,则
,则![]() .
.
因为![]() ,则
,则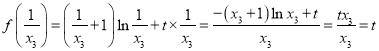 ,
,
所以![]() ,从而
,从而![]() ,即②正确.
,即②正确.
由上面可知![]() ,所以③正确.
,所以③正确.
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目