Question

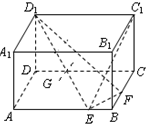如图，在长方体ABCD-A₁B₁C₁D₁中，已知AB=4，AD=3，AA₁=2，E，F分别是棱AB，BC上的点，且EB=FB=1．
（1）求异面直线EC₁与FD₁所成角的余弦值；
（2）试在面ABCD上确定一点G，使G到平面D₁EF距离为

11

11

．

Answer 1

分析：（1）以D为原点，DA，DC，DD₁分别为x轴、y轴、z轴建立空间直角坐标系，得用向量法能求出异面直线EC₁与FD₁所成角的余弦值．
（2）由D₁（0，0，2），E（3，3，0），F（2，4，0），知

D1E

=（3，3，-2），

D1F

=（2，4，-2），从而求出平面D₁EF垂直

n

=（1，1，3），再由G到平面D₁EF距离为

11

11

，能够在面ABCD上确定一点G．

解答：解：（1）以D为原点，DA，DC，DD₁分别为x轴、y轴、z轴建立空间直角坐标系，
∵AB=4，AD=3，AA₁=2，E，F分别是棱AB，BC上的点，且EB=FB=1，
∴D₁（0，0，2），E（3，3，0），F（2，4，0），C₁（0，4，2）．（1分）
∴

EC1

=（-3，1，2），

FD1

=（-2，-4，2）（3分）
∴异面直线EC₁与FD₁所成角的余弦值=|cos＜

EC1

，

FD1

＞|=|

6-4+4

14 • 24

|=

21

14

．
（2）∵D₁（0，0，2），E（3，3，0），F（2，4，0），
∴

D1E

=（3，3，-2），

D1F

=（2，4，-2），
设向量

n

=（x，y，z）与平面D₁EF垂直，则有

n

•

D1E

=0，

n

•

D1F

=0，
∴

3x+3y-2z=0 2x+4y-2z=0

，解得

n

=（1，1，3），
设在面ABCD上确定一点G（a，b，0），则

EG

=（a-3，b-3，0），
∵G到平面D₁EF距离为

11

11

，
∴

|a-3+b-3|

11

=

11

11

，
∴a+b-6=1，即b=7-a．
故在面ABCD上确定一点G（a，7-a，0），使G到平面D₁EF距离为

11

11

．

点评：本题考查异面直线所成的角的余弦值求法，考查点到平面的距离的求法及其应用，解题时要认真审题，注意等价转化思想的合理运用．