题目内容
13.在极坐标系中,过点$(2,-\frac{π}{6})$且平行于极轴的直线的方程是( )| A. | ρcosθ=$\sqrt{3}$ | B. | ρcosθ=-$\sqrt{3}$ | C. | ρsinθ=1 | D. | ρsinθ=-1 |
分析 利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$化为直角坐标,即可得出.
解答 解:点$(2,-\frac{π}{6})$化为直角坐标$(2cos(-\frac{π}{6}),2sin(-\frac{π}{6}))$,即$(\sqrt{3},-1)$.
∴过点$(2,-\frac{π}{6})$且平行于极轴的直线的方程是y=-1,
化为直角坐标方程为:ρsinθ=-1.
故选:D.
点评 本题考查了极坐标与直角坐标互化公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
2.下列说法错误的是( )
| A. | 设有一个回归方程为$\widehat{y}$=3-5x,则变量x每增加一个单位,y平均增加5个单位 | |
| B. | 回归直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点($\overline{x}$,$\overline{y}$) | |
| C. | 在一个2×2列联表中,由计算得随机变量K2的观测值k=13.079,则可以在犯错误的概率不超过0.001的前提下,认为这两个变量间有关系 | |
| D. | 将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变 |
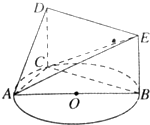 如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=$\frac{1}{2}$.
如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=$\frac{1}{2}$.