题目内容
5.已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1及点P(1,$\frac{1}{2}$),过点P作直线l与椭圆C交于A、B两点,过A、B两点分别作C的切线交于点Q.(1)求点Q的轨迹方程;
(2)求△ABQ的面积的最小值.
分析 (1)设A(x1,y1),B(x2,y2),Q(x0,y0),因为AQ与圆C相切,求得AQ的方程为$\frac{{x}_{1}x}{2}$+y1y=1,同理可得BQ的方程为$\frac{{x}_{2}x}{2}$+y2y=1,由直线都过点Q,即可得到所求轨迹方程;
(2)易得当直线AB和Q的轨迹平行时,面积最小,求得两直线的距离和弦长AB,由面积公式计算即可得到所求值.
解答 解:设A(x1,y1),B(x2,y2),Q(x0,y0),
因为AQ与椭圆C相切,
对椭圆C:$\frac{{x}^{2}}{2}$+y2=1两边对x取导数,可得x+2y•y′=0,
可得y′=-$\frac{x}{2y}$,即有AQ的方程为y-y1=-$\frac{{x}_{1}}{2{y}_{1}}$(x-x1),
又$\frac{{{x}_{1}}^{2}}{2}$+y12=1,即有AQ的方程为$\frac{{x}_{1}x}{2}$+y1y=1,
同理可得BQ的方程为$\frac{{x}_{2}x}{2}$+y2y=1,
由于AQ,BQ都过点Q,
所以过点A,B的直线方程为$\frac{{x}_{0}x}{2}$+y0y=1,
因直线AB过点(1,$\frac{1}{2}$).
所以代入得$\frac{1}{2}$x0+$\frac{1}{2}$y0=1,
所以点Q的轨迹方程为:x+y=2;
(2)可得当直线AB和Q的轨迹平行时,面积最小,
设直线AB的方程为y-$\frac{1}{2}$=-(x-1),即有y=-x+$\frac{3}{2}$,
代入椭圆方程可得6x2-12x+5=0,
即有x1+x2=2,x1x2=$\frac{5}{6}$,
则弦长AB=$\sqrt{1+1}$•$\sqrt{{2}^{2}-\frac{20}{6}}$=$\frac{2\sqrt{3}}{3}$,
由平行线的距离公式可得d=$\frac{|2-\frac{3}{2}|}{\sqrt{2}}$=$\frac{1}{2\sqrt{2}}$,
即有△ABQ的面积的最小值为$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$×$\frac{1}{2\sqrt{2}}$=$\frac{\sqrt{6}}{12}$.
点评 本题考查椭圆方程的应用,考查直线和椭圆相切的条件,考查轨迹方程的求法,以及运算求解能力,属于中档题.

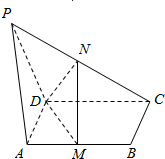 如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点.
如图,PA⊥平面ABCD,ABCD是矩形,M、N分别是AB,PC的中点. 如图,在三棱锥S-ABC中,SA⊥平面ABC,∠ABC=90°,SA=BC=2,AB=4,M,N,D分别是SC,AB,BC的中点.
如图,在三棱锥S-ABC中,SA⊥平面ABC,∠ABC=90°,SA=BC=2,AB=4,M,N,D分别是SC,AB,BC的中点.