题目内容
17.已知数列{an}满足an+1=an+2(n∈N+)且a1,a3,a7成等比.(1)求数列{an}的通项公式.
(2)设数列{bn}满足bn+1-bn=an(n∈N+)且b1=2,求数列$\left\{{\frac{1}{b_n}}\right\}$得前n项的和.
分析 (1)通过an+1=an+2(n∈N+)易知数列{an}为公差d=2的等差数列,利用a1,a3,a7成等比计算可知a1=4,进而可得结论;
(2)通过(1)可知bn+1-bn=2n+2(n∈N+),进而bn-bn-1=2n(n≥2,且n∈N+)、bn-1-bn-2=2n-2、…、b2-b1=4,累加、裂项可知$\frac{1}{{b}_{n}}$=$\frac{1}{n}$-$\frac{1}{n+1}$,进而并项相加即得结论.
解答 解:(1)∵an+1=an+2(n∈N+),
∴数列{an}为公差d=2的等差数列,
又∵a1,a3,a7成等比,
∴${({a_1}+4)^2}={a_1}•({a_1}+12)$,
解得a1=4,
∴an=2n+2;
(2)由(1)可知bn+1-bn=2n+2(n∈N+),
∴bn-bn-1=2n(n≥2,且n∈N+),
bn-1-bn-2=2n-2,
…
b2-b1=4,
累加得:bn-b1=2•$\frac{(n-1)(2+n)}{2}$,
又∵b1=2,
∴bn=n(n+1),
∴$\frac{1}{{b}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
于是数列$\left\{{\frac{1}{b_n}}\right\}$得前n项的和为1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查数列的通项及前n项和,利用累加法及裂项相消法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
2.圆2x2+2y2+6x-4y-3=0的圆心坐标和半径分别为( )
| A. | (-$\frac{3}{2}$,1)和$\frac{19}{4}$ | B. | (3,2)和$\frac{\sqrt{19}}{2}$ | C. | (-$\frac{3}{2}$,1)和$\frac{\sqrt{19}}{2}$ | D. | ($\frac{3}{2}$,-1)和$\frac{\sqrt{19}}{2}$ |
7.函数$f(x)=\frac{1}{{\sqrt{1-x}}}$的定义域是( )
| A. | [1,+∞) | B. | (-∞,1) | C. | (-∞,1] | D. | (1,+∞) |
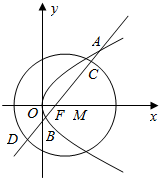 如图,抛物线C1:y2=2px(p>0)和圆C2:(x-1)2+y2=r2(r>0),M为圆C2的圆心,过抛物线C1的焦点F的直线y=k(x-$\frac{p}{2}$)与C1交于A,B两点,与圆C2交与C,D两点(点C在A,B之间)且△AOF的外心到抛物线C1的准线的距离为$\frac{3}{4}$.
如图,抛物线C1:y2=2px(p>0)和圆C2:(x-1)2+y2=r2(r>0),M为圆C2的圆心,过抛物线C1的焦点F的直线y=k(x-$\frac{p}{2}$)与C1交于A,B两点,与圆C2交与C,D两点(点C在A,B之间)且△AOF的外心到抛物线C1的准线的距离为$\frac{3}{4}$.