��Ŀ����
����Ŀ����ͼ��OM��ON�����������ߣ�QΪ����һ��С����AΪ������OM�ϵ�һ����ͷ����֪![]() ��
��![]() ��Q��������OM��ON�ľ���ֱ�Ϊ3 km��
��Q��������OM��ON�ľ���ֱ�Ϊ3 km��![]() km����Ҫ�ں�����ON���ٽ�һ����ͷ��ʹ����ˮ������ֱ��AB����С��Q��
km����Ҫ�ں�����ON���ٽ�һ����ͷ��ʹ����ˮ������ֱ��AB����С��Q��
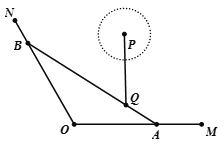
��1����ˮ��������AB�ij���
��2����С�������������С��6 km���ĺ�����һ��Բ��ǿˮ��P����ˮ������t hʱ�İ뾶Ϊ![]() ��aΪ������ij�������ǿˮ����ʼ����ʱ��һ������
��aΪ������ij�������ǿˮ����ʼ����ʱ��һ������![]() km/h���ٶ�����ͷA������ͷB����ʵ��a��ʲô��Χȡֵʱ��ǿˮ�����Შ�����ֵĺ��У�
km/h���ٶ�����ͷA������ͷB����ʵ��a��ʲô��Χȡֵʱ��ǿˮ�����Შ�����ֵĺ��У�
���𰸡���1��![]() ��2��
��2��![]()
��������
���⣨1������������ֱ������ϵ��Ϊ�����ʾ��![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ����Q��������ON�ľ���Ϊ
����Q��������ON�ľ���Ϊ![]() km����
km����![]() �����
�����![]() ��������ֱ�߽����
��������ֱ�߽����![]() �������������빫ʽ��
�������������빫ʽ��![]() ��2����������һ������ʽ��������⣺��
��2����������һ������ʽ��������⣺��![]() Сʱʱ���������߶�
Сʱʱ���������߶�![]() �ϵĵ�
�ϵĵ�![]() ����
����![]() ������ʽ����������������ñ������뽫��ת��Ϊ��Ӧ������ֵ���⣺
������ʽ����������������ñ������뽫��ת��Ϊ��Ӧ������ֵ���⣺![]()
�����������1���Ե�![]() Ϊ����ԭ�㣬ֱ��
Ϊ����ԭ�㣬ֱ��![]() Ϊ
Ϊ![]() �ᣬ����ֱ������ϵ��ͼ��ʾ��
�ᣬ����ֱ������ϵ��ͼ��ʾ��

��������ã�![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
��![]() ����
����![]() ��
��![]() ����
����![]() ����ֱ��
����ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ����
����![]() �� ��
�� ��![]() ��
��![]() ��
��![]() ����
����![]() ����ˮ��������
����ˮ��������![]() �ij�Ϊ
�ij�Ϊ![]() ��
��
��2�������������ǿˮ��Բ![]() ��������ɵ�P��3��9��������
��������ɵ�P��3��9��������![]() Сʱʱ���������߶�
Сʱʱ���������߶�![]() �ϵĵ�
�ϵĵ�![]() ������
������![]() ����
����![]() ��ǿˮ�����Შ�����ֵĺ��м�
��ǿˮ�����Შ�����ֵĺ��м�![]()
![]() ����
����![]() ʱ ��
ʱ ��![]() ��
��![]()
![]() .
.![]() ��
��![]() �����ҽ���
�����ҽ���![]() ʱ�Ⱥų��������ԣ���
ʱ�Ⱥų��������ԣ���![]() ʱ
ʱ![]() ��������༴ǿˮ�����Შ�����ֵĺ��У�
��������༴ǿˮ�����Შ�����ֵĺ��У�

 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�