题目内容
【题目】若椭圆
的焦点在x轴上，离心率为
，依次连接的四个顶点所得四边形的面积为40.
（1）试求的标准方程；
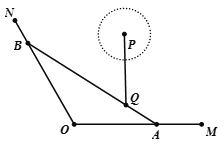
（2）若曲线M上任意一点到的右焦点的距离与它到直线
的距离相等，直线
经过的下顶点和右顶点，
，直线
与曲线M相交于点P、Q（点P在第一象限内，点Q在第四象限内），设的下顶点是B，上顶点是D，且
，求直线的方程.
【答案】（1）
；（2）
【解析】
(1)根据条件列出关于
的等式构建方程组求解出，即可求解出椭圆的标准方程；
(2)根据抛物线的定义可求
的轨迹方程，利用直线
联立的轨迹方程得到韦达定理形式，再根据三角形的面积比求解出直线的方程.
（1）由题意可知：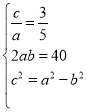
解得
，∴所求
的标准方程是；
（2）由（1）可知的右焦点是
，下顶点
，上顶点
，右顶点是
又由抛物线定义可知：曲线M是一条抛物线，M的焦点是
∴M的方程是
，又
，
∴
，∴
，设直线的方程为
则联立方程组：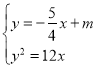
，消去
得：
，
且
，所以
，所以
，
所以由韦达定理得：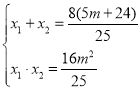
，又由
可得
，即：
∴联立方程组：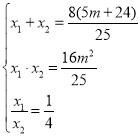
，解得：
，或
又∵点P在第一象限内，点Q在第四象限内，∴不合，舍去
∴所求直线的方程为
，即：.
练习册系列答案
相关题目
