题目内容
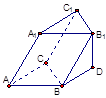
若两条异面直线所成的角为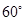 ,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有( )
,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有( )
| A.12对 | B.18对 | C.24对 | D.30对 |
C
解析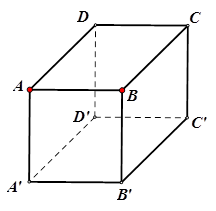
试题分析:与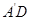 所成的角为
所成的角为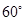 的异面直线有四对,即:
的异面直线有四对,即: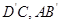 ,
,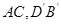 ;与
;与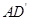 所成的角为
所成的角为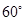 的异面直线有四对,即:
的异面直线有四对,即: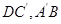 ,
,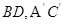 ;与
;与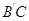 所成的角为
所成的角为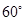 的异面直线有四对,即:
的异面直线有四对,即: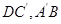 ,
,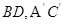 ;与
;与 所成的角为
所成的角为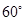 的异面直线有四对,即:
的异面直线有四对,即: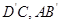 ,
,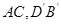 ;与
;与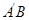 所成的角为
所成的角为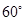 的异面直线有两对,即:
的异面直线有两对,即: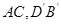 ;与
;与 所成的角为
所成的角为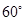 的异面直线有两对,即:
的异面直线有两对,即: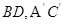 ;与
;与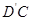 所成的角为
所成的角为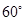 的异面直线有两对,即:
的异面直线有两对,即: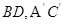 ;与
;与 所成的角为
所成的角为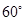 的异面直线有两对,即:
的异面直线有两对,即: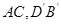 ,综上所述:“黄金异面直线对”共有24对.
,综上所述:“黄金异面直线对”共有24对.
考点:异面直线.

练习册系列答案
相关题目
设 是两个不同的平面,
是两个不同的平面, 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
从正方体六个面的对角线中任取两条作为一对,其中所成的角为 的共有( )
的共有( )
| A.24对 | B.30对 | C.48对 | D.60对 |
已知是两条不同直线,是两个不同的平面,给出下列命题:
①若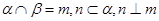 ,则
,则 ;②若
;②若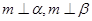 ,则
,则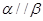 ;③若
;③若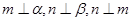 ,则
,则 ;④若
;④若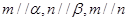 ,则
,则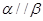 ,其中正确的命题是( )
,其中正确的命题是( )
| A.①② | B.②③ | C.③④ | D.①③ |
设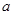 、
、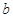 是两条不同的直线,
是两条不同的直线,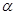 、
、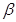 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A.若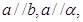 则 则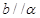 | B.若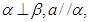 则 则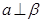 |
C.若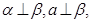 则 则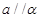 | D.若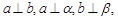 则 则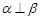 |
[2012·安徽高考]设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |

 的侧棱
的侧棱 在下底面的射影
在下底面的射影 与
与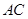 平行,若
平行,若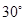 ,且
,且 ,则
,则 的余弦值为( )
的余弦值为( )