题目内容
已知各项均不为零的数列{an},定义向量 .下列命题中真命题是
.下列命题中真命题是
 .下列命题中真命题是
.下列命题中真命题是A.若 n∈N*总有 n∈N*总有 ∥ ∥ 成立,则数列{an}是等差数列; 成立,则数列{an}是等差数列; |
B.若 n∈N*总有 n∈N*总有 ∥ ∥ 成立,则数列{an}是等比数列; 成立,则数列{an}是等比数列; |
C.若 n∈N*总有 n∈N*总有 ⊥ ⊥ 成立,则数列{an}是等差数列; 成立,则数列{an}是等差数列; |
D.若 n∈N*总有 n∈N*总有 ⊥ ⊥ 成立,则数列{an}是等比数列. 成立,则数列{an}是等比数列. |
A
试题分析:因为
 n∈N*总有
n∈N*总有 ∥
∥ 成立,所以
成立,所以 =0,
=0, ;
;从而
 ,所以
,所以 ,
, ,即数列{an}是等差数列,故选A。
,即数列{an}是等差数列,故选A。点评:简单题,准确计算向量的数量积是基础,利用“累乘法”是关键。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 ,且
,且 依次是等比数列
依次是等比数列 的前两项。
的前两项。
 且
且 ,使得数列
,使得数列 是常数列?若存在,求出
是常数列?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。 满足
满足
 ; (Ⅱ)证明
; (Ⅱ)证明 .
. 中,
中, ,
, ,记
,记 为
为 项的和,则
项的和,则 = ;
= ; 满足
满足 ,
, ,则数列
,则数列 .
.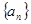 的通项公式
的通项公式 其前
其前 项和
项和 ,则
,则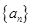 满足
满足 ,
, (
(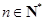 ),则
),则 的值为 .
的值为 .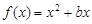 的图象在点
的图象在点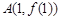 处的切线
处的切线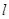 与直线
与直线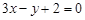 平行,若数
平行,若数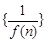 的前
的前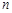 项和为
项和为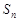 ,则
,则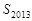 的值为 .
的值为 .  为
为 ,
, ,
, ,
, ,…….若
,…….若 ,则
,则 的前几项和
的前几项和 = ( )
= ( )


