题目内容
【题目】在四棱锥P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,AD=6,PA⊥底面ABCD,E是PD上的动点.若CE∥平面PAB,则三棱锥C﹣ABE的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系, A(0,0,0),B(0,2,0),C(2,2,0),D(6,0,0),P(0,0,3),
设E(a,0,c), ![]() ,则(a,0,c﹣3)=(6λ,0,﹣3λ),
,则(a,0,c﹣3)=(6λ,0,﹣3λ),
解得a=6λ,c=3﹣3λ,∴E(6λ,0,3﹣3λ),![]() =(6λ﹣2,﹣2,3﹣3λ),
=(6λ﹣2,﹣2,3﹣3λ),
平面ABP的法向量 ![]() =(1,0,0),
=(1,0,0),
∵CE∥平面PAB,∴ ![]() =6λ﹣2=0,
=6λ﹣2=0,
解得 ![]() ,∴E(2,0,2),
,∴E(2,0,2),
∴E到平面ABC的距离d=2,
∴三棱锥C﹣ABE的体积:
VC﹣ABE=VE﹣ABC= ![]() =
= ![]() =
= ![]() .
.
故选:D.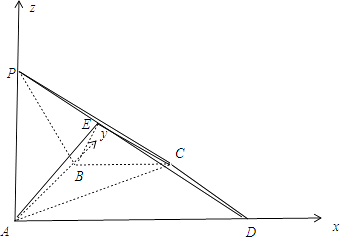
以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出三棱锥C﹣ABE的体积.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目