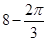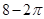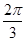题目内容
一个体积为 的正方体的顶点都在球面上,则球的表面积是 ( )
的正方体的顶点都在球面上,则球的表面积是 ( )
A. | B. | C. | D. |
B
解析试题分析:因为正方体的体积为 ,所以棱长为
,所以棱长为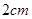 ,因为正方体的定点都在球面上,所以正方体的体对角线应该为球的直径,所以球的直径为
,因为正方体的定点都在球面上,所以正方体的体对角线应该为球的直径,所以球的直径为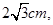 所以球的半径为
所以球的半径为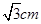 ,所以球的表面积为
,所以球的表面积为
考点:本小题主要考查正方体与其外接球的关系和球的表面积的计算,考查学生的运算求解能力.
点评:正方体外接于球,则正方体的体对角线为球的直径;如果球内切于正方体,则正方体的棱长等于球的直径.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
下列结论正确的是( )
| A.各个面都是三角形的几何体是三棱锥 |
| B.以三角形一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥 |
| C.棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥 |
| D.圆锥的顶点与底面圆周上的任意一点的连线都是母线 |
三棱锥的三条侧棱两两垂直,其长分别是1、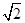 、
、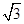 ,则此三棱锥的外接球的表面积是( )
,则此三棱锥的外接球的表面积是( )
| A.6π | B.5π | C.4π | D.9π |
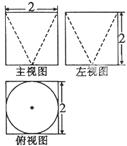
如图是某一几何体的三视图,则这个几何体的体积为( )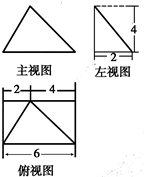
| A.4 | B.8 | C.16 | D.20 |
已知正三棱柱ABC—A1B1C1中,A1B⊥CB1,则A1B与AC1所成的角为( )
| A.450 | B.600 | C.900 | D.1200 |
 ,∠ASC=∠BSC=30°,则棱锥SABC的体积为( )
,∠ASC=∠BSC=30°,则棱锥SABC的体积为( ) 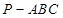 中,底面
中,底面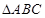 是边长为2的正三角形,
是边长为2的正三角形, 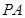 ⊥底面
⊥底面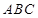 ,且
,且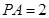 ,则此三棱锥外接球的半径为( )
,则此三棱锥外接球的半径为( )