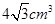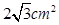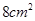题目内容
三棱锥的三条侧棱两两垂直,其长分别是1、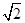 、
、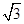 ,则此三棱锥的外接球的表面积是( )
,则此三棱锥的外接球的表面积是( )
| A.6π | B.5π | C.4π | D.9π |
A
解析试题分析:三棱锥的三条侧棱两两互相垂直,所以它的外接球就是它扩展为长方体的外接球,
所以求出长方体的对角线的长为 ,故球的直径为
,故球的直径为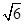 ,半径为
,半径为 ,所以球的表面积为:6π.故答案为A
,所以球的表面积为:6π.故答案为A
考点:本题主要是考查球的表面积,几何体的外接球,考查空间想象能力,计算能力,是基础题.
点评:解决该试题的关键是理解三棱锥的三条侧棱两两互相垂直,它的外接球就是它扩展为长方体的外接球,求出长方体的对角线的长,就是球的直径,然后求球的表面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个几何体的三视图如图所示,已知这几何体的体积为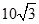 ,则
,则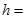 ( )
( )
A.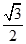 | B.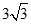 | C. | D. |
( )球的表面积与它的内接正方体的表面积之比是
A.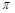 | B.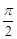 | C.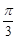 | D.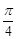 |
设四棱锥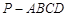 的底面不是平行四边形,用平面
的底面不是平行四边形,用平面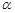 去截此四棱锥,使得截面是平行四边形,则这样的平面
去截此四棱锥,使得截面是平行四边形,则这样的平面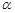 ( )
( )
| A.不存在 | B.有且只有1个 | C.恰好有4个 | D.有无数多个 |
一个体积为 的正方体的顶点都在球面上,则球的表面积是 ( )
的正方体的顶点都在球面上,则球的表面积是 ( )
A. | B. | C. | D. |
如右图所示,正三棱锥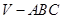 中,
中,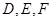 分别是
分别是  的中点,
的中点, 为
为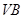 上任意一点,则直线
上任意一点,则直线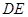 与
与 所成的角的大小是( )
所成的角的大小是( )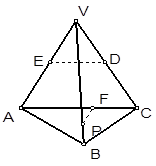
A. | B. |
C.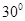 | D.随 点的变化而变化。 点的变化而变化。 |
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点
上有两个动点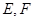 ,且
,且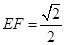 ,则下列结论中错误的是( )
,则下列结论中错误的是( )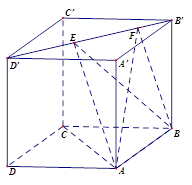
A.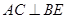 |
B.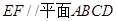 |
C.三棱锥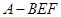 的体积为定值 的体积为定值 |
D.异面直线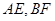 所成的角为定值 所成的角为定值 |
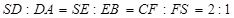 ,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )
,若仍用该容器盛水,最多盛水(可以任意情形放置)为原三棱锥体积的( )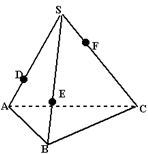
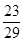
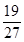
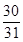
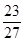
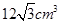 ,其三视图中的俯视图如图所示,则其侧(左)视图的面积是( )
,其三视图中的俯视图如图所示,则其侧(左)视图的面积是( )