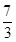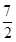题目内容
已知球的直径SC=4,A,B是该球球面上的两点,AB= ,∠ASC=∠BSC=30°,则棱锥SABC的体积为( )
,∠ASC=∠BSC=30°,则棱锥SABC的体积为( )
A.3 | B.2 | C. | D.1 |
C
解析试题分析:
取SC的中点D,则D为球心,则AD=BD=DS=2,∠ASC=∠BSC=∠SBD=300,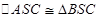 过A做AE⊥SC与E,连接BE,则BE⊥SC.在∆BDE中,DE=BDcos∠BED=1,BE=BDsin∠BED=
过A做AE⊥SC与E,连接BE,则BE⊥SC.在∆BDE中,DE=BDcos∠BED=1,BE=BDsin∠BED= ,故三棱锥SABC的体积等于棱锥SABE和棱锥CABE的体积之和,即
,故三棱锥SABC的体积等于棱锥SABE和棱锥CABE的体积之和,即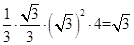 。
。
考点:棱锥的体积公式;球的有关性质。
点评:求三棱锥的体积关键是确定底面和高。一般的时候,找一个易求高的底面。属于中档题。

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
正方体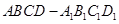 中,
中, 与平面
与平面 所成角的余弦值为( )
所成角的余弦值为( )
A. | B.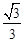 | C. | D.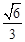 |
把3个半径为R的铁球熔化铸成一个底面半径为R的圆柱(不计损耗),则圆柱的高为( )
A. | B.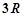 | C. | D.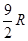 |
一个几何体的三视图及其尺寸(单位:cm) ,如图所示,则该几何体的体积为( ) .
. 
| A.144 | B.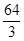 | C. | D.64 |
一个几何体的三视图如图所示,已知这几何体的体积为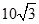 ,则
,则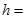 ( )
( )
A.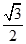 | B.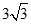 | C. | D. |
某几何体的三视图如下,则几何体的表面积为( )。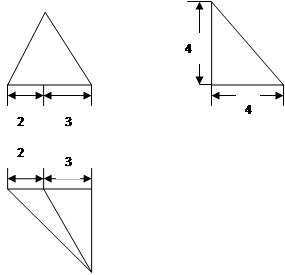
A.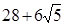 | B.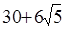 |
C.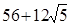 | D. |
一个体积为 的正方体的顶点都在球面上,则球的表面积是 ( )
的正方体的顶点都在球面上,则球的表面积是 ( )
A. | B. | C. | D. |
 )
)