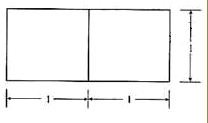
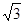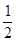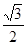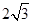题目内容
下列各图是正方体或正四面体,P,Q,R,S分别是所在棱的中点,这四个点中不共面的一个图是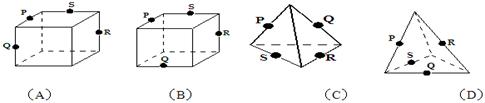
D
解析试题分析:选项A中,由于PQ,SR都是中位线,那么延长之后可以相交,故是共面。选项B中,QR,PS的延长线,符合中位线的性质,延长后相交于一点,故是共面的四点。而选项C中,PS,QR,都平行与同一条直线,那么可知共面,排除法选D.
考点:本题主要考查了空间中线面的位置关系的共面问题的运用。
点评:解决该试题的关键是连接直线,运用中位线的性质,以及平行四边形的性质,判定四点是否为共面,然后确定是否为异面直线,进而得到结论。

练习册系列答案
相关题目
一个体积为 的正方体的顶点都在球面上,则球的表面积是 ( )
的正方体的顶点都在球面上,则球的表面积是 ( )
A. | B. | C. | D. |
如右图所示,正三棱锥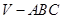 中,
中,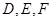 分别是
分别是  的中点,
的中点, 为
为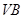 上任意一点,则直线
上任意一点,则直线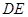 与
与 所成的角的大小是( )
所成的角的大小是( )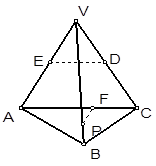
A. | B. |
C.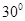 | D.随 点的变化而变化。 点的变化而变化。 |
若正四棱柱 的底面边长为1,
的底面边长为1, 与底面
与底面 成60°角,则
成60°角,则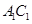 到底面
到底面 的距离为 ( )
的距离为 ( )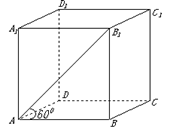
A. | B.1 | C. | D. |
长方体ABCD—A B
B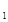 CD中,
CD中, ,
,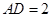 ,
,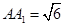 ,则点
,则点 到平面
到平面 的距离是( )
的距离是( )
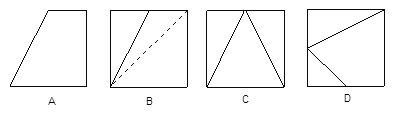
A. | B.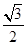 | C.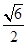 | D.2 |
三视图如右图的几何体是
| A.三棱锥 | B.四棱锥 |
| C.四棱台 | D.三棱台 |

 ,
,