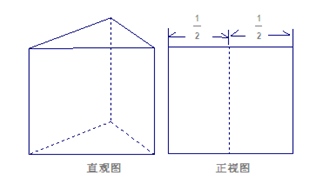
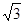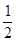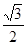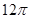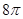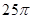题目内容
已知正三棱柱ABC—A1B1C1中,A1B⊥CB1,则A1B与AC1所成的角为( )
| A.450 | B.600 | C.900 | D.1200 |
C.
解析试题分析:分别取AB,A1B1的中点M,N,连接B1M,AN,CM,C1N,因为此三棱柱为正三棱柱,所以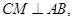
 又因为A1B⊥CB1,根据三垂线定理可知
又因为A1B⊥CB1,根据三垂线定理可知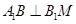 ,
,
因为四边形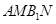 为平行四边形,所以AN//B1M,所以再由三垂线定理的逆定理可知
为平行四边形,所以AN//B1M,所以再由三垂线定理的逆定理可知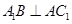 ,所以A1B与AC1所成的角为900.
,所以A1B与AC1所成的角为900.
考点:三垂线定理及逆定理.
点评:解本小题关键是在平面A1ABB1内作出B1C,AC1的射影,然后再利用三垂线定理或逆定理进行证明即可.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
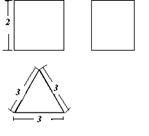
某几何体的三视图如下,则几何体的表面积为( )。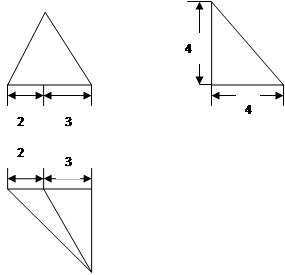
A.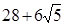 | B.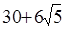 |
C.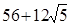 | D. |
( )球的表面积与它的内接正方体的表面积之比是
A.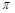 | B.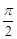 | C.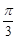 | D.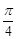 |
一个体积为 的正方体的顶点都在球面上,则球的表面积是 ( )
的正方体的顶点都在球面上,则球的表面积是 ( )
A. | B. | C. | D. |
如右图所示,正三棱锥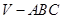 中,
中,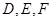 分别是
分别是  的中点,
的中点, 为
为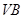 上任意一点,则直线
上任意一点,则直线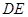 与
与 所成的角的大小是( )
所成的角的大小是( )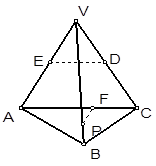
A. | B. |
C.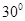 | D.随 点的变化而变化。 点的变化而变化。 |
长方体ABCD—A B
B CD中,
CD中, ,
,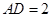 ,
,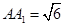 ,则点
,则点 到平面
到平面 的距离是( )
的距离是( )
A. | B.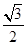 | C.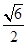 | D.2 |
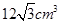 ,其三视图中的俯视图如图所示,则其侧(左)视图的面积是( )
,其三视图中的俯视图如图所示,则其侧(左)视图的面积是( )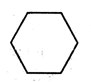
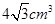
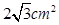
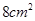
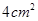
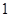 ,
,