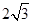题目内容
下列结论正确的是( )
| A.各个面都是三角形的几何体是三棱锥 |
| B.以三角形一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥 |
| C.棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥 |
| D.圆锥的顶点与底面圆周上的任意一点的连线都是母线 |
D
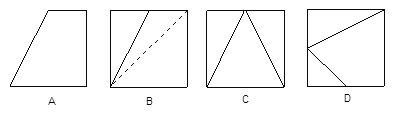
解析试题分析:A、如图(1)所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥,故A错误;
B、如图(2)(3)所示,若△ABC不是直角三角形,或是直角三角形但旋转轴不是直角边,所得的几何体都不是圆锥,故B错误;
C、若六棱锥的所有棱长都相等,则底面多边形是正六边形.由过中心和定点的截面知,若以正六边形为底面,侧棱长必然要大于底面边长,故C错误;
D、根据圆锥母线的定义知,故D正确. 故选D.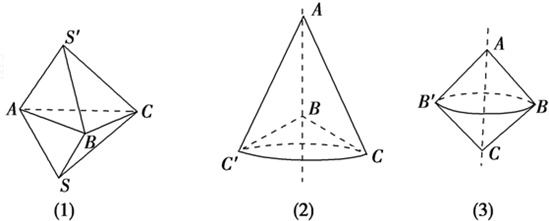
考点:空间几何体的结构特征。
点评:我们要充分把握每个空间几何体的结构特征。考查了空间想象能力。

练习册系列答案
相关题目
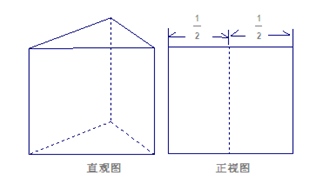
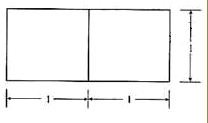
一个几何体的三视图及其尺寸(单位:cm) ,如图所示,则该几何体的体积为( ) .
. 
| A.144 | B.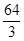 | C. | D.64 |
一个几何体的三视图如图所示,则该几何体的表面积为( )
A. | B.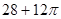 | C. | D. |
( )球的表面积与它的内接正方体的表面积之比是
A.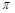 | B.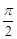 | C.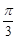 | D. |
一个体积为 的正方体的顶点都在球面上,则球的表面积是 ( )
的正方体的顶点都在球面上,则球的表面积是 ( )
A. | B. | C. | D. |






 ,
,