题目内容
【题目】某城市一社区接到有关部门的通知，对本社区居民用水量进行调研，通过抽样调查的方法获得了100户居民某年的月均用水量（单位：t），通过分组整理数据，得到数据的频率分布直方图如图所示：
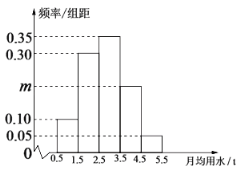
（Ⅰ）求图中m的值；并估计该社区居民月均用水量的中位数和平均值.（保留3位小数）
（Ⅱ）用此样本频率估计概率，若从该社区随机抽查3户居民的月均用水量，问恰有2户超过
的概率为多少？
（Ⅲ）若按月均用水量
和
分成两个区间用户，按分层抽样的方法抽取10户，每户出一人参加水价调整方案听证会.并从这10人中随机选取3人在会上进行陈述发言，设来自用水量在区间
的人数为X，求X的分布列和数学期望.
【答案】（Ⅰ）
，2.786，2.800；（Ⅱ）0.432；（Ⅲ）分布列见解析，
【解析】
（Ⅰ）根据频率分布直方图各小矩形面积和为1，即可求得m的值；根据频率分布直方图各小组的频率，由中位数定义即可求解；结合平均数的求法，可用频率分布直方图求得平均数.
（Ⅱ）先求得月均用水量超过
的概率，再结合独立重复试验中概率求法即可得恰有2户超过的概率.
（Ⅲ）按照分层抽样，先求得在月均用水量
和
在两个区间各自抽取的人数，可知来自用水量在区间
的人数为X的取值有0，1，2，3，分别求得各自对应的概率即可得分布列，由分布列求得数学期望即可.
（Ⅰ）由频率分布直方图得：
，
解得，
的频率为
，
的频率为0.35，
∴估计该社区居民月均用水量的中位数为：
平均值为：
.
（Ⅱ）用此样本频率估计概率，从该社区随机抽查3户居民的月均用水量，
月均用水量超过的概率为：
，
∴恰有2户超过的概率为
.
（Ⅲ）若按月均用水量和分成两个区间用户，按分层抽样的方法抽取10户，
月均用水量中抽取：
户，
月均用水量中抽取：
户.
从这10人中随机选取3人在会上进行陈述发言，设来自用水量在区间的人数为X，
则X的可能取值为0，1，2，3，
，
，
，
，
∴X的分布列为：
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
数学期望
.
